题目内容
若椭圆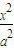
+y2=1（a＞0）的一条准线经过抛物线y2=-8x的焦点，则该椭圆的离心率为（ ）A．
B．
C．
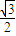
D．
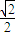
【答案】分析：由题意知椭圆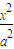
+y2=1（a＞0）的一条准线
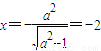，所以
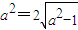，解可得：a2=2，c2=1．由此可求出椭圆的离心率．
解答：解：∵抛物线y2=-8x的焦点是（-2，0），
∴椭圆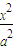
+y2=1（a＞0）的一条准线
，
∴
，
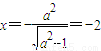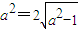∴a2=2，c2=1，
∴
．
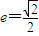故选D．
点评：本题考查椭圆的性质和应用，解题时要认真审题，仔细解答．
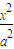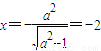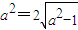+y2=1（a＞0）的一条准线，所以，解可得：a2=2，c2=1．由此可求出椭圆的离心率．解答：解：∵抛物线y2=-8x的焦点是（-2，0），
∴椭圆
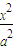+y2=1（a＞0）的一条准线，∴
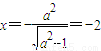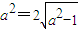，∴a2=2，c2=1，
∴
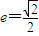．故选D．
点评：本题考查椭圆的性质和应用，解题时要认真审题，仔细解答．
练习册系列答案
阅读快车系列答案
相关题目
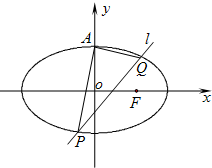如图，已知椭圆C：
+y2=1（a＞0）的一条准线经过抛物线y2=-8x的焦点，则该椭圆的离心率为
