题目内容
已知点B(0,1),A,C为椭圆C:
+y2=1(a>1)上的两点,△ABC是以B为直角顶点的直角三角形.
(1)△ABC能否为等腰三角形?若能,这样的三角形有几个?
(2)当a=2时,求线段AC的中垂线l在x轴上截距的取值范围.
| x2 | a2 |
(1)△ABC能否为等腰三角形?若能,这样的三角形有几个?
(2)当a=2时,求线段AC的中垂线l在x轴上截距的取值范围.
分析:(1)设出AB的方程为y=kx+1(不妨设k>0),BC的方程为y=-
x+1,利用直线与方程与椭圆方程联立,利用等腰直角三角形ABC中的两腰|AB|=|BC|,借助基本不等式即可求得a的取值范围;
(2)由a=2,可得椭圆的方程为
+y2=1.直线AC与x轴垂直时不符合题意.①直线AC的斜率为0时,线段AC的垂直平分线为y轴,即可得出线段AC的垂直平分线在x轴上的截距.
②设直线AC的方程为my=x+t.(m≠0),A(x1,y1),C(x2,y2).与椭圆的方程联立可得△>0及根与系数的关系,利用中点坐标公式可得线段AC的中点M的坐标,再利用相互垂直的直线斜率之间的关系可得线段AC的方程,进而求得线段BC的中垂线l在x轴上截距的取值范围.
| 1 |
| k |
(2)由a=2,可得椭圆的方程为
| x2 |
| 4 |
②设直线AC的方程为my=x+t.(m≠0),A(x1,y1),C(x2,y2).与椭圆的方程联立可得△>0及根与系数的关系,利用中点坐标公式可得线段AC的中点M的坐标,再利用相互垂直的直线斜率之间的关系可得线段AC的方程,进而求得线段BC的中垂线l在x轴上截距的取值范围.
解答:解:(1)不妨设lAB:y=kx+1(k>0),lBC:y=-
x+1.
由
,得(1+a2k2)x2+2ka2x=0,…①
∴|AB|=
|xA-xB|=
•
.
同理可得:|BC|=
•
=
•
.
由|AB|=|BC|得,k3-a2k2+a2k-1=0,
即(k-1)[k2+(1-a2)k+1]=0,解得k=1或k2+(1-a2)k+1=0.
对于k2+(1-a2)k+1=0,
由(1-a2)2-4=0,得a=
,此时方程的根k=1;
当1<a<
时,方程k2+(1-a2)k+1=0无实根;
当a>
时,方程k2+(1-a2)k+1=0有两个不等实数根.
∴当a>
时,这样的三角形有3个;当1<a≤
时这样的三角形有1个;
(2)由a=2,可得椭圆的方程为
+y2=1.
直线AC与x轴垂直时不符合题意.
①直线AC的斜率为0时,线段AC的垂直平分线为y轴,此时线段AC的垂直平分线在x轴上的截距为0.
②设直线AC的方程为my=x+t.(m≠0),A(x1,y1),C(x2,y2).
联立
,化为(4+m2)y2-2mty+t2-4=0.
∵直线AC与椭圆有两个交点,∴△=4m2t2-4(4+m2)(t2-4)>0,化为4+m2>t2.(*)
∴y1+y2=
,y1y2=
.(**)
设线段AC的中点M(x0,y0),则y0=
=
,x0=my0-t=
.
∴M(
,
).
∵AB⊥BC,
∴
•
=(x1,y1-1)•(x2,y2-1)=x1x2+(y1-1)(y2-1)
=(my1-t)(my2-t)+(y1-1)(y2-1)=(m2+1)y1y2-(mt+1)(y1+y2)+t2+1=0.
把(**)代入上式可得:
-
+t2+1=0,
化为 5t2-2mt-3m2=0,即(5t+3m)(t-m)=0.
解得t=m或t=-
.
当t=m时,直线AC化为m(y-1)=x过点(0,1),舍去.
当t=-
时,满足(*).
又线段AC的垂直平分线为:y-
=-m(x+
).
令y=0,得x=
,
把t=-
代入上式可得x=
=
,
当m>0时,0<x≤
.
当m<0时,-
≤m<0.
综上可知:线段AC的中垂线l在x轴上截距的取值范围是[-
,
].
| 1 |
| k |
由
|
∴|AB|=
| 1+k2 |
| 1+k2 |
| 2ka2 |
| 1+a2k2 |
同理可得:|BC|=
1+
|
| ||
1+
|
| 1+k2 |
| 2a2 |
| k2+a2 |
由|AB|=|BC|得,k3-a2k2+a2k-1=0,
即(k-1)[k2+(1-a2)k+1]=0,解得k=1或k2+(1-a2)k+1=0.
对于k2+(1-a2)k+1=0,
由(1-a2)2-4=0,得a=
| 3 |
当1<a<
| 3 |
当a>
| 3 |
∴当a>
| 3 |
| 3 |
(2)由a=2,可得椭圆的方程为
| x2 |
| 4 |
直线AC与x轴垂直时不符合题意.
①直线AC的斜率为0时,线段AC的垂直平分线为y轴,此时线段AC的垂直平分线在x轴上的截距为0.
②设直线AC的方程为my=x+t.(m≠0),A(x1,y1),C(x2,y2).
联立
|
∵直线AC与椭圆有两个交点,∴△=4m2t2-4(4+m2)(t2-4)>0,化为4+m2>t2.(*)
∴y1+y2=
| 2mt |
| 4+m2 |
| t2-4 |
| 4+m2 |
设线段AC的中点M(x0,y0),则y0=
| y1+y2 |
| 2 |
| mt |
| 4+m2 |
| -4t |
| 4+m2 |
∴M(
| -4t |
| 4+m2 |
| mt |
| 4+m2 |
∵AB⊥BC,
∴
| BA |
| BC |
=(my1-t)(my2-t)+(y1-1)(y2-1)=(m2+1)y1y2-(mt+1)(y1+y2)+t2+1=0.
把(**)代入上式可得:
| (m2+1)(t2-4) |
| 4+m2 |
| 2mt(mt+1) |
| 4+m2 |
化为 5t2-2mt-3m2=0,即(5t+3m)(t-m)=0.
解得t=m或t=-
| 3m |
| 5 |
当t=m时,直线AC化为m(y-1)=x过点(0,1),舍去.
当t=-
| 3m |
| 5 |
又线段AC的垂直平分线为:y-
| mt |
| 4+m2 |
| 4t |
| 4+m2 |
令y=0,得x=
| -3t |
| 4+m2 |
把t=-
| 3m |
| 5 |
| 9m |
| 5(4+m2) |
| ||
|
当m>0时,0<x≤
| 9 |
| 20 |
当m<0时,-
| 9 |
| 20 |
综上可知:线段AC的中垂线l在x轴上截距的取值范围是[-
| 9 |
| 20 |
| 9 |
| 20 |
点评:本题考查了直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、分类讨论、判别式与一元二次方程的实数根的关系、线段的垂直平分线等基础知识与基本技能方法,考查了推理能力、计算能力,考查了分析问题和解决问题的能力,属于难题.

练习册系列答案
相关题目
 的切线(P点不在y轴上).
的切线(P点不在y轴上).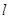 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使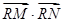 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。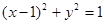 的切线(P点不在y轴上)
的切线(P点不在y轴上)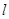 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使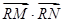 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。