题目内容
6.写出不大于1000的所有能被7整除的正整数,下面是四位同学设计的程序框图,其中正确的是( )| A. | 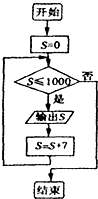 | B. |  | C. |  | D. |  |
分析 由1,2,…,1000的正整数,现需从中抽取能被7整除的作为样品进行检验,我们分析出程序的功能,进而分析出四个答案中程序流程图的执行结果,比照后,即可得到答案.
解答 解:由于程序的功能是从1,2,…,1000的正整数中,抽取所有能被7整除的为样品进行检验.
即抽取的结果为7,14,21,…,994,
A答案输出的结果为0,7,14,…,994,从0开始,故A不满足条件;
B答案输出的结果为7,14,21,…,994,故B满足条件;
C答案输出的结果为0,7,14,…,994,从0开始,到994结束,故C不满足条件;
D答案输出的结果为14,21,…,994,1001,到1001结束,故D不满足条件;
故选:B.
点评 本题考查的知识点是设计程序框图解决实际问题.分析程序框图的正确与否,可以逐一的对程序框图的功能,进行分析,如果符合题目要求,即为正确答案,如果程序运行的结果和题目要求不相符,即为错误.

练习册系列答案
相关题目
14.已知集合A={y|y=-x2+1,x∈R},B={y|y=log2x},则A∩B=( )
| A. | (-∞,1] | B. | R | C. | ∅ | D. | [1,+∞) |
11.我市“水稻良种研究所”对某水稻良种的发芽率与昼夜温差之间的关系进行研究.他们分别记录了3月21日至3月25日的昼夜温差及每天30颗水稻种子的发芽数,并得到如表资料
(1)请根据以上资料,求出y关于x的线性回归方程;据气象预报3月26日的昼夜温差为14℃,请你预测3月26日浸泡的30颗水稻种子的发芽数(结果保留整数).
(2)从3月21日至3月25日中任选2天,记种子发芽数超过15颗的天数为X,求X的概率分布列,并求其数学期望EX和方差DX.
(参考公式及参考数据b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$,a=$\overline{y}$-b$\overrightarrow{x}$,$\sum_{i}^{n}$xiyi=832,$\sum_{i}^{n}$xi2=615)
| 日期 | 3月21日 | 3月22日 | 3月23日 | 3月24日 | 3月25日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 9 |
| 发芽数y(颗) | 15 | 16 | 17 | 14 | 13 |
(2)从3月21日至3月25日中任选2天,记种子发芽数超过15颗的天数为X,求X的概率分布列,并求其数学期望EX和方差DX.
(参考公式及参考数据b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$,a=$\overline{y}$-b$\overrightarrow{x}$,$\sum_{i}^{n}$xiyi=832,$\sum_{i}^{n}$xi2=615)
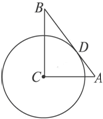 如图,在Rt△ABC中,斜边AB=5,直角边AC=4,如果以C为圆心的圆与AB相切于D,则⊙C的半径长为$\frac{12}{5}$.
如图,在Rt△ABC中,斜边AB=5,直角边AC=4,如果以C为圆心的圆与AB相切于D,则⊙C的半径长为$\frac{12}{5}$.