题目内容
16.已知命题p:在x∈[1,2]内,不等式x2-ax+2<0恒成立;命题q:函数f(x)=x2-2ax+3a是区间(-∞,1]上的减函数,若命题“p或q”是真命题,“p且q”是假命题,求实数a的取值范围.分析 若命题p是真命题:在x∈[1,2]内,不等式x2-ax+2<0恒成立,则$a>(x+\frac{2}{x})_{max}$,令g(x)=$x+\frac{2}{x}$,x∈[1,2],利用导数研究其单调性极值与最值即可得出g(x)max.若命题q是真命题:函数f(x)=x2-2ax+3a是区间(-∞,1]上的减函数,利用二次函数的单调性可得1≤a.若命题“p或q”是真命题,“p且q”是假命题,可得:命题p与q必然一真一假.
解答 解:若命题p是真命题:在x∈[1,2]内,不等式x2-ax+2<0恒成立,则$a>(x+\frac{2}{x})_{max}$,令g(x)=$x+\frac{2}{x}$,x∈[1,2],g′(x)=$1-\frac{2}{{x}^{2}}$=$\frac{{x}^{2}-2}{{x}^{2}}$,当x∈$[1,\sqrt{2})$时,g′(x)<0,函数g(x)单调递减;当x∈$(\sqrt{2},2]$时,g′(x)>0,函数g(x)单调递增.而g(1)=3,g(2)=3,∴g(x)max=3,∴a>3.
若命题q是真命题:函数f(x)=x2-2ax+3a是区间(-∞,1]上的减函数,则1≤a.
若命题“p或q”是真命题,“p且q”是假命题,
∴命题p与q必然一真一假.
∴$\left\{\begin{array}{l}{a>3}\\{a<1}\end{array}\right.$或$\left\{\begin{array}{l}{a≤3}\\{a≥1}\end{array}\right.$,
解得a∈∅或1≤a≤3.
∴实数a的取值范围是[1,3].
点评 本题考查了简易逻辑的判定方法、利用导数研究其单调性极值与最值、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
| A. | 25 | B. | 55 | C. | 72 | D. | 110 |
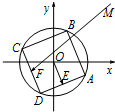 如图,已知圆O:x2+y2=4,M的坐标为(4,4),圆O的内接正方形ABCD的边AD,CD的中点分别为E,F,当正方形ABCD绕圆心O转动时,则$\overrightarrow{OE}•\overrightarrow{MF}$的取值范围是( )
如图,已知圆O:x2+y2=4,M的坐标为(4,4),圆O的内接正方形ABCD的边AD,CD的中点分别为E,F,当正方形ABCD绕圆心O转动时,则$\overrightarrow{OE}•\overrightarrow{MF}$的取值范围是( )| A. | [-4,4] | B. | $[-4\sqrt{2},4\sqrt{2}]$ | C. | [-8,8] | D. | $[-8\sqrt{2},8\sqrt{2}]$ |