题目内容
已知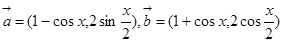
(Ⅰ)若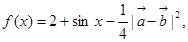 求
求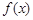 的表达式;
的表达式;
(Ⅱ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅲ)若 在
在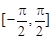 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
【答案】
(Ⅰ)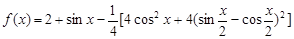
=2+sinx-cos2x-1+sinx=sin2x+2sinx ……………4分
(Ⅱ)设函数y=f (x)的图象上任一点M(x0,y0)关于原点的对称点为N(x,y)
则x0= -x,y0= -y
∵点M在函数y=f (x)的图象上
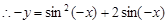 ,即y= -sin2x+2sinx
,即y= -sin2x+2sinx
∴函数g(x)的解析式为g(x)= -sin2x+2sinx ……………9分
(Ⅲ)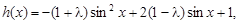 设sinx=t,(-1≤t≤1)
设sinx=t,(-1≤t≤1)
则有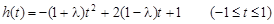
① 当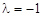 时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
② 当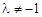 时,对称轴方程为直线
时,对称轴方程为直线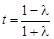 .
.
ⅰ) 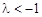 时,
时, ,解得
,解得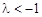
ⅱ)当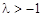 时,
时,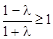 ,解得
,解得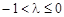
综上,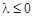 .
……………14分
.
……………14分
【解析】略

练习册系列答案
相关题目
某网站就观众对2010年春晚小品类节目的喜爱程度进行网上调查,其中持各种态度的人数如下表:
(1)现用分层抽样的方法从所有参与网上调查的观众中抽取了一个容量为n的样本,已知从不喜欢小品的观众中抽取的人数为5人,则n的值为多少?
(2)在(1)的条件下,若抽取到的5名不喜欢小品的观众中有2名为女性,现将抽取到的5名不喜欢小品的观众看成一个总体,从中任选两名观众,求至少有一名为女性观众的概率.
| 喜爱程度 | 喜欢 | 一般 | 不喜欢 |
| 人数 | 560 | 240 | 200 |
(2)在(1)的条件下,若抽取到的5名不喜欢小品的观众中有2名为女性,现将抽取到的5名不喜欢小品的观众看成一个总体,从中任选两名观众,求至少有一名为女性观众的概率.
已知10只狗的血球体积及红血球的测量值如下
|
|
|
| 45 | 6.53 |
| 42 | 6.30 |
| 46 | 9.25 |
| 48 | 7.50 |
| 42 | 6.99 |
| 35 | 5.90 |
| 58 | 9.49 |
| 40 | 6.20 |
| 39 | 6.55 |
| 50 | 7.72 |
![]() (血球体积,mm),
(血球体积,mm),![]() (红血球数,百万)
(红血球数,百万)
(1) 画出上表的散点图;
(2)求出回归直线并且画出图形;
(3)若血球体积为49mm,预测红血球数大约是多少?
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)请问是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交于不同两点
交于不同两点 ,
, ,且满足
,且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
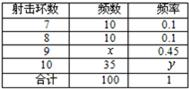
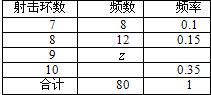
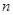 人,成绩只有
人,成绩只有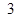 、
、 、
、 三种分值,设
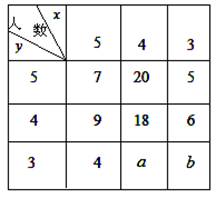
三种分值,设 分别表示项目A与项目B成绩.例如:表中项目A成绩为
分别表示项目A与项目B成绩.例如:表中项目A成绩为 且
且 的概率是
的概率是 .
.
 名礼仪小姐,则
名礼仪小姐,则 的礼仪小姐中应抽多少人?
的礼仪小姐中应抽多少人? ,
, ,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.
,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.




