题目内容
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)请问是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交于不同两点
交于不同两点 ,
, ,且满足
,且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(1)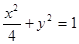 ,
,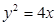 ;(2)
;(2)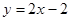 或
或 .
.
【解析】本试题主要考查了抛物线的方程以及直线与抛物线的位置关系。
解:(1)设抛物线 :
: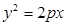
 ,则有
,则有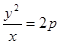 ,据此验证4个点知
,据此验证4个点知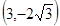 ,
,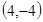 在抛物线上,易求
在抛物线上,易求 :
: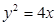 .
.
设 :
: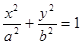 ,把点
,把点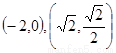 代入得
代入得
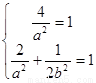 ,解得,
,解得,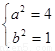 ,
,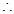
 的方程为:
的方程为: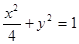 .
.
综上, 的方程为:
的方程为: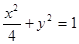 ,
, 的方程为:
的方程为: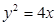 。
。
(2)假设存在这样的直线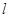 ,设其方程为
,设其方程为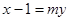 ,两交点坐标为
,两交点坐标为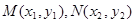 ,
,
由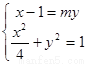 消去
消去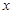 ,得
,得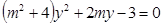 ,
,
 ①
①

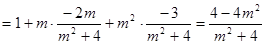 ,②
,②

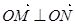 ,
,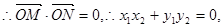 ③
③
将①②代入③得,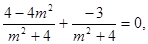 解得
解得
所以假设成立,即存在直线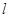 满足条件,且
满足条件,且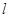 的方程为
的方程为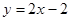 或
或 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上各取两个点,将其坐标记录于下表中:
,从每条曲线上各取两个点,将其坐标记录于下表中:
|
| 3 | 2 | 4 |
|
|
|
| 0 | 4 |
|
⑴求![]() 的标准方程;
的标准方程;
⑵是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知椭圆 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)设斜率不为0的动直线 与
与 有且只有一个公共点
有且只有一个公共点 ,且与
,且与 的准线交于
的准线交于 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出
?若存在,求出 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
已知椭圆 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为坐标原点
的顶点均为坐标原点 ,从每条曲线上各取两个点,将其坐标记录于表中:
,从每条曲线上各取两个点,将其坐标记录于表中:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求 的标准方程;
的标准方程;
(2)请问是否存在直线 同时满足条件:(ⅰ)过
同时满足条件:(ⅰ)过 的焦点
的焦点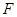 ;(ⅱ)与
;(ⅱ)与 交于不同两点
交于不同两点 、
、 ,且满足
,且满足 .若存在,求出直线
.若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上各取两个点,将其坐标记录于下表中:
,从每条曲线上各取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
⑴求 的标准方程;
的标准方程;
⑵是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交不同两点
交不同两点 且满足
且满足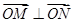 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.














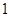









 2
2


 [
[