题目内容
在平面直角坐标系中,若不等式组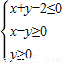 所表示的平面区域上恰有两个点在圆x2+(y-b)2=r2(r>0)上,则( )
所表示的平面区域上恰有两个点在圆x2+(y-b)2=r2(r>0)上,则( )A.b=0,

B.b=1,r=1
C.b=-1,
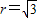
D.b=-1,

【答案】分析:确定不等式组表示的平面区域,利用条件,可得(2,0),(1,1)在圆上,由此可得结论.
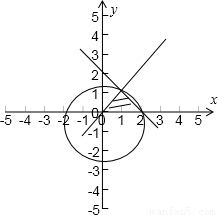
解答:解:不等式组表示的平面区域如图所示,三角形三个顶点的坐标为(0,0),(2,0),(1,1)
∵不等式组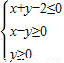 所表示的平面区域上恰有两个点在圆x2+(y-b)2=r2(r>0)上,
所表示的平面区域上恰有两个点在圆x2+(y-b)2=r2(r>0)上,
∴(2,0),(1,1)在圆上
∴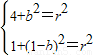
∴b=-1,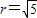
故选D.
点评:本题考查线性规划知识,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.
解答:解:不等式组表示的平面区域如图所示,三角形三个顶点的坐标为(0,0),(2,0),(1,1)

∵不等式组
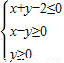 所表示的平面区域上恰有两个点在圆x2+(y-b)2=r2(r>0)上,
所表示的平面区域上恰有两个点在圆x2+(y-b)2=r2(r>0)上,∴(2,0),(1,1)在圆上
∴
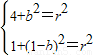
∴b=-1,
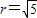
故选D.
点评:本题考查线性规划知识,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目