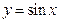题目内容
(1)求函数y=sin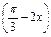 的单调递减区间;
的单调递减区间;
(2)求y=3tan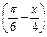 的周期及单调区间.
的周期及单调区间.
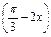 的单调递减区间;
的单调递减区间;(2)求y=3tan
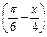 的周期及单调区间.
的周期及单调区间.(1)函数的单调递减区间为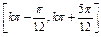 (k∈Z)
(k∈Z)
(2)y=3tan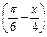 的单调递减区间是
的单调递减区间是 (k∈Z)
(k∈Z)
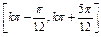 (k∈Z)
(k∈Z)(2)y=3tan
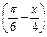 的单调递减区间是
的单调递减区间是 (k∈Z)
(k∈Z)(1)方法一 令u=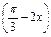 ,y=sinu,利用复合函数单调性,
,y=sinu,利用复合函数单调性,
由2k -
-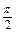 ≤-2x+
≤-2x+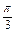 ≤2k
≤2k +
+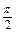 (k∈Z),得
(k∈Z),得
2k -
- ≤-2x≤2k
≤-2x≤2k +
+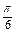 (k∈Z),
(k∈Z),
-k -
-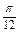 ≤x≤-k
≤x≤-k +
+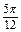 (k∈Z),
(k∈Z),
即k -
-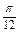 ≤x≤k
≤x≤k +
+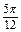 (k∈Z).
(k∈Z).
∴原函数的单调递减区间为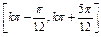 (k∈Z).
(k∈Z).
方法二 由已知函数y=-sin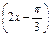 ,欲求函数的单调递减区间,只需求y=sin
,欲求函数的单调递减区间,只需求y=sin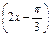 的单调递增区间.
的单调递增区间.
由2k -
-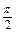 ≤2x-
≤2x-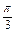 ≤2k
≤2k +
+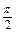 (k∈Z),
(k∈Z),
解得k -
-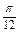 ≤x≤k
≤x≤k +
+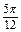 (k∈Z).
(k∈Z).
∴原函数的单调递减区间为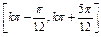 (k∈Z).
(k∈Z).
(2)y=3tan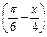 =-3tan
=-3tan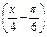 ,
,
∴T=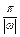 =4
=4 ,∴y=3tan
,∴y=3tan 的周期为4
的周期为4 .
.
由k -
-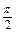 <
<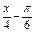 <k
<k +
+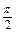 ,
,
得4k -
-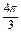 <x<4k
<x<4k +
+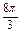 (k∈Z),
(k∈Z),
y=3tan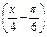 的单调增区间是
的单调增区间是
 (k∈Z)
(k∈Z)
∴y=3tan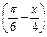 的单调递减区间是
的单调递减区间是 (k∈Z).
(k∈Z).
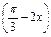 ,y=sinu,利用复合函数单调性,
,y=sinu,利用复合函数单调性,由2k
 -
-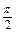 ≤-2x+
≤-2x+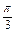 ≤2k
≤2k +
+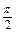 (k∈Z),得
(k∈Z),得2k
 -
- ≤-2x≤2k
≤-2x≤2k +
+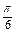 (k∈Z),
(k∈Z),-k
 -
-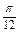 ≤x≤-k
≤x≤-k +
+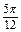 (k∈Z),
(k∈Z),即k
 -
-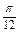 ≤x≤k
≤x≤k +
+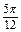 (k∈Z).
(k∈Z).∴原函数的单调递减区间为
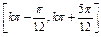 (k∈Z).
(k∈Z).方法二 由已知函数y=-sin
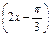 ,欲求函数的单调递减区间,只需求y=sin
,欲求函数的单调递减区间,只需求y=sin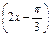 的单调递增区间.
的单调递增区间.由2k
 -
-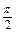 ≤2x-
≤2x-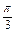 ≤2k
≤2k +
+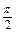 (k∈Z),
(k∈Z),解得k
 -
-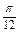 ≤x≤k
≤x≤k +
+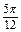 (k∈Z).
(k∈Z).∴原函数的单调递减区间为
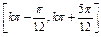 (k∈Z).
(k∈Z).(2)y=3tan
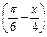 =-3tan
=-3tan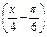 ,
,∴T=
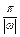 =4
=4 ,∴y=3tan
,∴y=3tan 的周期为4
的周期为4 .
.由k
 -
-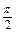 <
<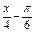 <k
<k +
+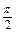 ,
,得4k
 -
-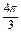 <x<4k
<x<4k +
+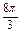 (k∈Z),
(k∈Z),y=3tan
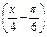 的单调增区间是
的单调增区间是 (k∈Z)
(k∈Z)∴y=3tan
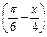 的单调递减区间是
的单调递减区间是 (k∈Z).
(k∈Z).
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
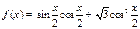 .
.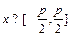 时,求f (
时,求f (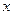 )的值域;
)的值域;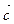 ="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量
="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量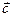 .
.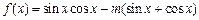 .
.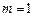 ,求函数
,求函数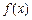 在
在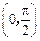 上的单调增区间;
上的单调增区间;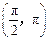 上是单调递减函数,求实数
上是单调递减函数,求实数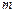 的取值范围.
的取值范围. 。
。 时,求函数f(x)的最大值、最小值。
时,求函数f(x)的最大值、最小值。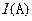 随时间
随时间 变化的函数为
变化的函数为 .
. 时的电流强度.
时的电流强度.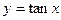 得到曲线
得到曲线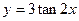 的变化过程,并求出坐标伸缩变换.
的变化过程,并求出坐标伸缩变换.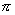 为周期、在
为周期、在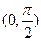 上单调递增的偶函数是
上单调递增的偶函数是  的图象只需将
的图象只需将 的图象 ( )
的图象 ( ) 个单位
个单位 个单位
个单位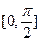 上为减函数的是
上为减函数的是