Question

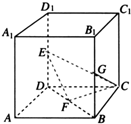如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，点E、F、G分别是DD₁，BD，BB₁的中点．
（1）求证：EF⊥CF；
（2）求EF与CG所成角的余弦值；
（3）求CE的长．

Answer 1

分析：（1）利用线面垂直的判定证明CF⊥平面BDD₁B₁，再利用线面垂直的性质证明EF⊥CF；
（2）取B₁D₁的中点M，连接GM，CM，B₁D．在平面BB₁DD₁上，FE∥B₁D，GM∥B₁D，所以∠CGM（或其补角）为EF与CG所成角，故可求；
（3）直接利用勾股定理计算可得．

解答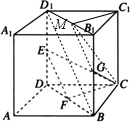：（1）证明：在棱长为1的正方体ABCD-A₁B₁C₁D₁中，∵F是BD的中点
∴CF⊥BD，D₁D⊥CF
∵BD∩D₁D=D
∴CF⊥平面BDD₁B₁，
∵点E、F分别是DD₁，BD的中点．
∴EF?平面BDD₁B₁，
∴EF⊥CF；
（2）取B₁D₁的中点M，连接GM，CM，B₁D．
在平面BB₁DD₁上，FE∥B₁D，GM∥B₁D，所以∠CGM（或其补角）为EF与CG所成角．
在△CMG中，MG=

3

2

，CG=

1+ 1 4

=

5

2

，CM=

1+ 1 2

=

6

2

∴cos∠CGM=

3 4 + 5 4 - 6 4

2× 3 2 × 5 2

=

15

15

∴EF与CG所成角的余弦值为

15

15

；
（3）在直角△DEC中，CD=1，DE=

2

2

，∴CE=

1+ 1 4

=

5

2

点评：本题重点考查线面垂直的判定与性质，考查线线角，熟练掌握线面垂直的判定与性质是关键．