题目内容
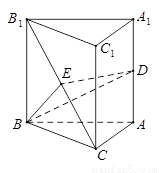
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.(1)求证:DE∥平面ABC;
(2)求证:B1C⊥平面BDE.
分析:(1)取BC中点G,连接AG,EG,欲证直线DE∥平面ABC,只需证明DE平行平面ABC中的一条直线即可,由四边形ADEG为平行四边形,可知AG∥DE,AG?平面ABC,DE?平面ABC,问题得证.
(2)取BC的中点G,判断三棱柱ABC-A1B1C1为直三棱柱,BB1⊥平面ABC,再证明B1C⊥BE,可证得:B1C⊥平面BDE.
(2)取BC的中点G,判断三棱柱ABC-A1B1C1为直三棱柱,BB1⊥平面ABC,再证明B1C⊥BE,可证得:B1C⊥平面BDE.
解答: 证明:(1),
证明:(1),
∵G,E分别为CB,CB1的中点,
∴EG∥BB1,且EG=
AA1,
又∵正三棱柱ABC-A1B1C1,
∴EG∥AD,EG=AD
∴四边形ADEG为平行四边形.
∴AG∥DE
∵AG?平面ABC,DE?平面ABC,
所以 DE∥平面ABC.
(2)由可得,取BC中点G
∵正三棱柱ABC-A1B1C1,
∴BB1⊥平面ABC.
∵AG?平面ABC,
∴AG⊥BB1,
∵G为BC的中点,AB=AC,
∴AG⊥BC∴AG⊥平面BB1C1C,
∵B1C?平面BB1C1C,
∴AG⊥B1C,
∵AG∥DE
∴DE⊥B1C,
∵BC=BB1,B1E=EC
∴B1C⊥BE,
∵BE?平面BDE,DE?平面BDEBE∩DE=E,
∴B1C⊥平面BDE.
 证明:(1),
证明:(1),∵G,E分别为CB,CB1的中点,
∴EG∥BB1,且EG=
| 1 |
| 2 |
又∵正三棱柱ABC-A1B1C1,
∴EG∥AD,EG=AD
∴四边形ADEG为平行四边形.
∴AG∥DE
∵AG?平面ABC,DE?平面ABC,
所以 DE∥平面ABC.
(2)由可得,取BC中点G
∵正三棱柱ABC-A1B1C1,
∴BB1⊥平面ABC.
∵AG?平面ABC,
∴AG⊥BB1,
∵G为BC的中点,AB=AC,
∴AG⊥BC∴AG⊥平面BB1C1C,
∵B1C?平面BB1C1C,
∴AG⊥B1C,
∵AG∥DE
∴DE⊥B1C,
∵BC=BB1,B1E=EC
∴B1C⊥BE,
∵BE?平面BDE,DE?平面BDEBE∩DE=E,
∴B1C⊥平面BDE.
点评:本题主要考查了证明线面平行的方法、空间的线面平行,线线垂直的证明,充分考查了学生的逻辑推理能力,空间想象力,以及识图能力.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
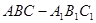 中,
中,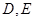 分别为
分别为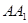 ,
,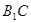 的中点.
的中点.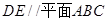 ;
;
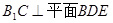 .
.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
