题目内容
（本小题满分12分）
已知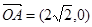
，
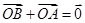，O为坐标原点，动点E满足:
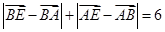
（Ⅰ） 求点E的轨迹C的方程；
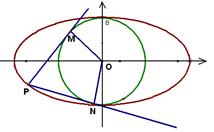
（Ⅱ）过曲线C上的动点P向圆O：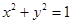
引两条切线PA、PB，切点分别为A、B，直线AB与x轴、y轴分别交于M、N两点，求ΔMON面积的最小值.
【答案】
（1）
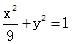；（2）
.
【解析】
试题分析：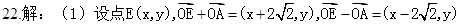
，
，
，
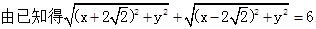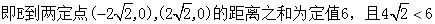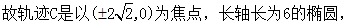
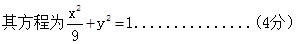
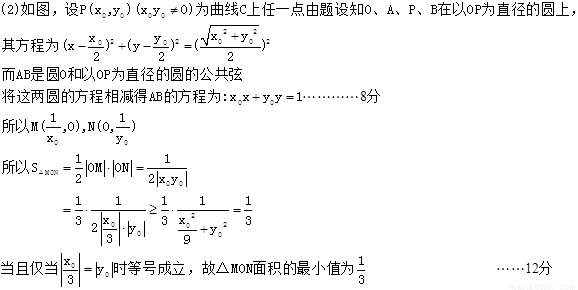
考点：本题主要考查椭圆的定义，椭圆的标准方程，直线与圆的位置关系，基本不等式的应用。
点评：中档题，本题以平面向量为工具，利用向量模的几何意义，明确了点的轨迹是椭圆，并运用椭圆的定义及几何性质求得椭圆标准方程。往往通过联立圆的方程，得到公共弦方程，为进一步解题奠定了基础。利用函数思想，得到三角形面积表达式，利用基本不等式求得面积的最值。
练习册系列答案
导学全程练创优训练系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
