题目内容
(本小题满分12分)已知函数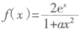 (e为自然对数的底数).
(e为自然对数的底数).
(I )若函数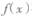 有极值,求实数a的取值范围;
有极值,求实数a的取值范围;
(II)若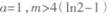 ,求证:当x>0时,
,求证:当x>0时,
【答案】
(Ⅰ) 由 ,可得
,可得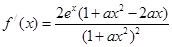 ,………………….2分
,………………….2分
依题意,需方程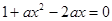 在
在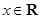 上有两个不等实根,
上有两个不等实根,
则: ,…………………4分
,…………………4分
解得: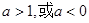 .
……………………5分
.
……………………5分
(Ⅱ)若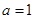 ,
,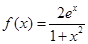 ,
,
∴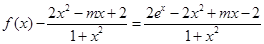 ,
,
设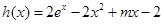 ,
,
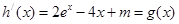 ,
,
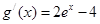 , ………………………7分
, ………………………7分
令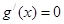 , 得
, 得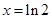 .
.
当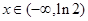 时,
时, 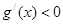 ,
,  单调递减;
单调递减;
当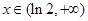 时,
时,  ,
,  单调递增;
单调递增;
∴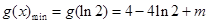 ,
,
∴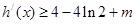 ,…………………9分
,…………………9分
∵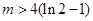 ,∴
,∴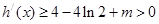 ,
,
∴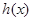 在
在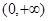 上单调递增, ∵
上单调递增, ∵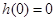 ,
,
∴ 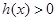 ,
……………………………11分
,
……………………………11分
∵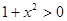 , ∴
, ∴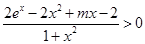 ,
,
∴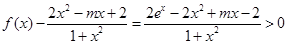 ,
,
即 .
……………………12分
.
……………………12分
【解析】(I)连续函数有极值,说明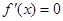 的方程有根。并且根两侧的导数值异号。根据这一点确定a的取值范围。
的方程有根。并且根两侧的导数值异号。根据这一点确定a的取值范围。
(II)把要证的不等式转化为:当x>0时,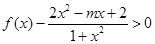 恒成立的问题。然后根据条件再构造函数求最值进行求证。
恒成立的问题。然后根据条件再构造函数求最值进行求证。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目