题目内容
已知直角 的三边长
的三边长 ,满足
,满足
(1)在 之间插入2011个数,使这2013个数构成以
之间插入2011个数,使这2013个数构成以 为首项的等差数列
为首项的等差数列 ,且它们的和为
,且它们的和为 ,求的最小值;
,求的最小值;
(2)已知 均为正整数,且
均为正整数,且 成等差数列,将满足条件的三角形的面积从小到大排成一列
成等差数列,将满足条件的三角形的面积从小到大排成一列 ,且
,且 ,求满足不等式
,求满足不等式 的所有
的所有 的值;
的值;
(3)已知 成等比数列,若数列
成等比数列,若数列 满足
满足 ,证明:数列
,证明:数列 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且 是正整数.
是正整数.
(1)最小值为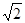 ; (2) 2、3、4.
; (2) 2、3、4.
(3)证明:由 成等比数列,
成等比数列, .
.
由于 为直角三角形的三边长,证明数列
为直角三角形的三边长,证明数列 中的任意连续三项为边长均可以构成直角三角形. 证得
中的任意连续三项为边长均可以构成直角三角形. 证得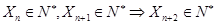 ,
,
故对于任意的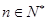 都有
都有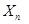 是正整数.
是正整数.
解析试题分析:(1) 是等差数列,∴
是等差数列,∴ ,即
,即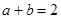 . 2分
. 2分
所以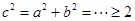 ,的最小值为
,的最小值为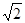 ; 4分
; 4分
(2) 设 的公差为
的公差为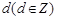 ,则
,则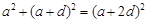
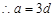 5分
5分
设三角形的三边长为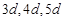 ,面积
,面积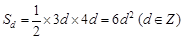 ,
,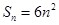 ,
,
 . 7分
. 7分
由 得
得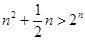 ,
,
当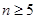 时,
时,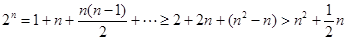 ,
,
经检验当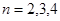 时,
时,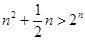 ,当
,当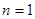 时,
时,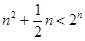 9分
9分
综上所述,满足不等式 的所有
的所有 的值为2、3、4. 10分
的值为2、3、4. 10分
(3)证明:因为 成等比数列,
成等比数列, .
.
由于 为直角三角形的三边长,知
为直角三角形的三边长,知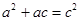 ,
,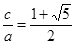 , 11分
, 11分
又 ,得
,得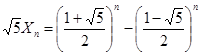 ,
,
于是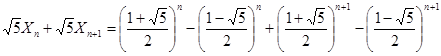
 .… 12分
.… 12分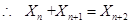 ,则有
,则有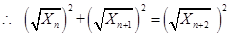 .
.
故数列 中的任意连续三项为边长均可以构成直角三角形. 14分
中的任意连续三项为边长均可以构成直角三角形. 14分
因为 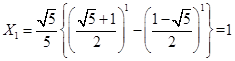 ,
,
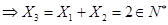 , 15分
, 15分
由 ,同理可得
,同理可得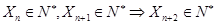 ,
,
故对于任意的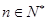 都有
都有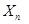 是正整数. 16分
是正整数. 16分
考点:本题主要考查等差数列、等比数列的基础知识,构成直角三角形的条件。
点评:难题,本题综合性较强,涉及等差数列、等比数列、不等式及构成直角三角形的条件。对法则是自点变形能力要求高,易出错。

练习册系列答案
相关题目
在等差数列{an}中,其前n项和是 ,若
,若 ,则在
,则在 中最大的是( )
中最大的是( )
A. | B. | C. | D. |
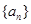 的前
的前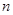 项和
项和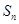 满足
满足 ,
,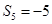 。
。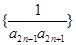 的前
的前 的前
的前 项和为
项和为 ,
,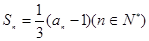
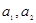 ;
; 的各项都是正数,且满足:
的各项都是正数,且满足: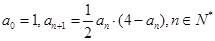
 ;
;
 中,角
中,角 、
、 、
、 成等差数列,且
成等差数列,且 .
.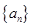 满足
满足 ,前
,前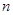 项为和
项为和 ,若
,若 ,求
,求 的前
的前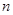 项和为
项和为 .
. ;
; 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,且对任意的
项和,且对任意的 ,有
,有 .
. ,求数列
,求数列 的前
的前 .
.  是等差数列,
是等差数列, ,数列
,数列 的前n项和是
的前n项和是 ,且
,且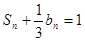 .
.