��Ŀ����
����Ŀ��ij���������˾ÿ��ƻ����������������ɡ����������߹� ![]() ��������һ��������
��������һ�������� ![]() ���ӣ�����һ�������
���ӣ�����һ������� ![]() ���ӣ�����һ��ɡ����
���ӣ�����һ��ɡ���� ![]() ���ӣ���֪������ʱ�䲻����
���ӣ���֪������ʱ�䲻���� ![]() Сʱ��������һ�������ɻ�����
Сʱ��������һ�������ɻ����� ![]() Ԫ������һ������ɻ�����
Ԫ������һ������ɻ����� ![]() Ԫ������һ��ɡ���ɻ�����
Ԫ������һ��ɡ���ɻ����� ![]() Ԫ.
Ԫ.
��1����ÿ���������������� ![]() ���������
��������� ![]() ��ʾÿ�������
��ʾÿ������� ![]() ��Ԫ����
��Ԫ����
��2����ô���������������ʹÿ������������������Ƕ��٣�
���𰸡�
��1���⣺������ÿ��������ɡ������Ϊ100��x��y��
��������w��5x��6y��3��100��x��y����2x��3y��300
��2���⣺Լ������Ϊ 
������ 
Ŀ�꺯��Ϊw��2x��3y��300.
������������ͼ��ʾ��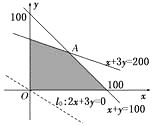
��ʼֱ��l0��2x��3y��0��ƽ�Ƴ�ʼֱ�߾�����Aʱ��w�����ֵ��
�� ![]() ��
�� ![]()
���Ž�ΪA��50,50��������wmax��550Ԫ��
����ÿ����������50�������50����ɡ��0��ʱ��������Ϊ����550Ԫ
��������������Ŀ���������������ص㣬������������x�����������y����������ɡ����100-x-y��������������Ϊz=5x+6y+3��100-x-y��=2x+3y+300����������ʱ����������������г�Լ������������ƽ�����������Թ滮֪ʶ������Ž⣮�����˼����Թ滮��Ӧ�ã��г�Լ���������ó�Ŀ�꺯���ǽ���Ĺؼ���