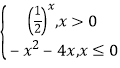题目内容
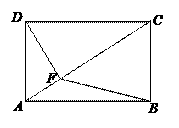
【题目】如图,矩形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 是
是 ![]() 上的动点.现将矩形
上的动点.现将矩形 ![]() 沿着对角线
沿着对角线 ![]() 折成二面角
折成二面角 ![]() ,使得
,使得 ![]() .
.
(Ⅰ)求证:当 ![]() 时,
时, ![]() ;
;
(Ⅱ)试求 ![]() 的长,使得二面角
的长,使得二面角 ![]() 的大小为
的大小为 ![]() .
.
【答案】解:(Ⅰ)连结 ![]() ,
, ![]() .
.
在矩形 ![]() 中,
中, ![]() ,
,![]() ,
, ![]() .
.
在 ![]() 中,∵
中,∵ ![]() ,
,![]() ,
,
∵ ![]() ,
,![]() ,即
,即 ![]() .
.
又在 ![]() 中,
中,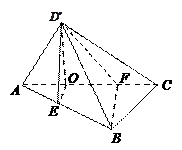
![]() ,
,
∴在 ![]() 中,
中, ![]() ,
,![]() ,
,
又 ![]() ,
,
∴ ![]() 平面
平面 ![]() .
.
∴ ![]() .
.
(Ⅱ)解:在矩形 ![]() 中,过
中,过 ![]() 作
作 ![]() 于
于 ![]() ,并延长交
,并延长交 ![]() 于
于 ![]() . 沿着对角线
. 沿着对角线 ![]() 翻折后,
翻折后,
由(Ⅰ)可知, ![]() 两两垂直,
两两垂直,
以 ![]() 为原点,
为原点, ![]() 的方向为
的方向为 ![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系 ![]() ,则
,则![]()
![]() ,
,![]() 平面
平面 ![]() ,
,![]() 为平面
为平面 ![]() 的一个法向量.
的一个法向量.
设平面 ![]() 的法向量为
的法向量为 ![]()
![]() ,
, ![]() ,
,
由 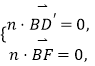 得
得 ![]()
取 ![]() 则
则 ![]() ,
, ![]() .
. 即
即 ![]() ,
,![]() .
.![]() 当
当 ![]() 时,二面角
时,二面角 ![]() 的大小是
的大小是 ![]()
【解析】(Ⅰ)根据题目中所给的条件的特点,连结DF,BF.通过计算推出DF⊥AC,得到D'F⊥AC,然后证明D'F⊥平面ABC.推出利用线面垂直的性质得到D'F⊥BC.
(Ⅱ)先说明OE,OC,OD'两两垂直,以O为原点,建立适当的空间直角坐标系O-xyz,求出平面AD'F的一个法向量.以及平面BD'F的法向量,通过用空间向量求平面间的夹角的方法,利用向量的数量积求解二面角的平面角的余弦值即可.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目