题目内容
在平面直角坐标系中，i，j分别是与x轴、y轴正方向同向的单位向量，O为坐标原点，设向量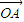
=2i+j，
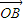=3i+kj，若A，O，B三点不共线，且△AOB有一个内角为直角，则实数k的所有可能取值的个数是（ ）A．1
B．2
C．3
D．4
【答案】分析：根据△AOB有一个内角为直角，进行分类讨论，根据两向量垂直则两向量的数量积为零建立方程，分别求出各种情形下的k的值即可．
解答：解：当∠AOB为直角时，
即（2i+j）（3i+kj）=6+k=0，解得k=-6；
当∠OAB为直角时，
即（2i+j）[i+（k-1）j]=2+k-1=0，解得k=-1；
当∠OBA为直角时，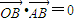
即（3i+kj）[i+（k-1）j]=3+k（k-1）=0，无解；
k可取的值有2个；
故选B．
点评：本题主要考查了单位向量，以及向量在几何中的应用和分类讨论的数学思想，属于基础题．
解答：解：当∠AOB为直角时，
即（2i+j）（3i+kj）=6+k=0，解得k=-6；当∠OAB为直角时，
即（2i+j）[i+（k-1）j]=2+k-1=0，解得k=-1；当∠OBA为直角时，
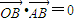即（3i+kj）[i+（k-1）j]=3+k（k-1）=0，无解；k可取的值有2个；
故选B．
点评：本题主要考查了单位向量，以及向量在几何中的应用和分类讨论的数学思想，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目