题目内容
【题目】斐波那契数列(![]() )又称黄金分割数列,因数学家列昂纳多斐波那契(
)又称黄金分割数列,因数学家列昂纳多斐波那契(![]() )以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列
)以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由题目![]() ,可列举该数列,该数列每项被3除以后的余数是周期为8的有序数字,每一个周期里面有两个0,即每个周期里面有两个数字可以被3整除,利用古典概型公式可得数列的前2024项中能被3整除的概率.
,可列举该数列,该数列每项被3除以后的余数是周期为8的有序数字,每一个周期里面有两个0,即每个周期里面有两个数字可以被3整除,利用古典概型公式可得数列的前2024项中能被3整除的概率.
![]() ,即该数列从第三项起,每一项均为前两项数字的和,
,即该数列从第三项起,每一项均为前两项数字的和,
∴数列为1,1,2,3,5,8,13,21,34,55,89,144,233,……,
该数列每项被3除后的余数分别为1,1,2,0,2,2,1,0,1,1,2,0,……,
可以发现余数是周期为8的有序数字,每一个周期里面有两个0,
即每个周期里面有两个数字可以被3整除,前2024项里面共有![]() (个)周期,
(个)周期,
∴有![]() (个)数字可以被3整除,
(个)数字可以被3整除,
记“从该数列的前2024项中随机抽取一项,能被3整除”为事件A,
则![]() ,
,
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
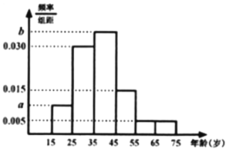
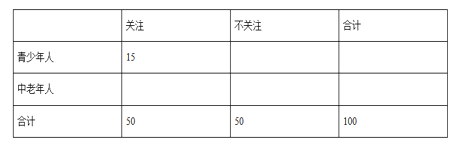
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好