题目内容
15.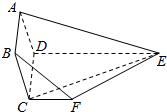 如图所示,在多面体ABCDEF中,四边形ABCD为矩形,底面CDEF为直角梯形,且平面ABCD⊥平面CDEF,CF∥DE,CD⊥DE,AB=2BC=2CF=2,DE=3CF.
如图所示,在多面体ABCDEF中,四边形ABCD为矩形,底面CDEF为直角梯形,且平面ABCD⊥平面CDEF,CF∥DE,CD⊥DE,AB=2BC=2CF=2,DE=3CF.(1)试问:线段AE上是否存在一点P,使得PF∥平面ABCD?请说明理由;
(2)若P是AE的中点,求三棱锥P-CEF的体积.
分析 (1)如图所示,线段AE上存在一点P,使得PF∥平面ABCD.分别在AE,AD上取一点P,N,使得$\frac{AP}{AE}=\frac{AN}{AD}$=$\frac{1}{3}$,连接PN.可得PN=$\frac{1}{3}$DE=1,PN∥DE,已知CF∥DE,CF=$\frac{1}{3}$DE.即可证明四边形PNCF是平行四边形,再利用线面平行的判定定理即可证明.
(2)四边形ABCD为矩形,平面ABCD⊥平面CDEF,可得:AD⊥平面CDEF,在直角梯形CDEF中,可得S△CEF=$\frac{1}{2}CF•CD$,又P是AE的中点,VP-CEF=$\frac{1}{2}{V}_{A-CEF}$=$\frac{1}{2}$×$\frac{1}{3}{S}_{△CEF}$•AD,即可得出.
解答 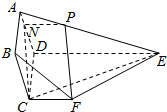 (1)解:如图所示,线段AE上存在一点P,使得PF∥平面ABCD.
(1)解:如图所示,线段AE上存在一点P,使得PF∥平面ABCD.
分别在AE,AD上取一点P,N,使得$\frac{AP}{AE}=\frac{AN}{AD}$=$\frac{1}{3}$,连接PN.
则PN=$\frac{1}{3}$DE=1,PN∥DE,又CF∥DE,CF=$\frac{1}{3}$DE.
∴PN$\underset{∥}{=}$CF,
∴四边形PNCF是平行四边形,
∴PF∥CN,又NC?平面ABCD,PF?平面ABCD,
∴PF∥平面ABCD.
(2)解:∵四边形ABCD为矩形,平面ABCD⊥平面CDEF,
∴AD⊥平面CDEF,
在直角梯形CDEF中,∵CD⊥CF.
∴S△CEF=$\frac{1}{2}CF•CD$=$\frac{1}{2}×1×1$=$\frac{1}{2}$.又P是AE的中点,
∴VP-CEF=$\frac{1}{2}{V}_{A-CEF}$=$\frac{1}{2}$×$\frac{1}{3}{S}_{△CEF}$•AD
=$\frac{1}{6}×\frac{1}{2}×1$
=$\frac{1}{12}$.
点评 本题考查了空间线面面面的位置关系、平行线与平行四边形的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{65}{3}$ | B. | $\frac{\sqrt{65}}{3}$ | C. | $\frac{31}{6}$ | D. | $\frac{65}{6}$ |
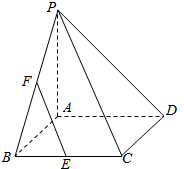 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA=AB,PA⊥平面ABCD,E,F分别是BC,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA=AB,PA⊥平面ABCD,E,F分别是BC,PB的中点.