题目内容
有以下4个命题:①定义在R上的函数f(x)满足f(2)>f(1),则函数f(x)在R上不是减函数;
②函数f(x)=lg
| x2+1 |
| |x| |
③函数f(x)=x+
| 1 |
| x |
④已知函数f(x)的定义域为[a,b],且a<c<b,当x∈[a,c]时,f(x)是单调增函数,又当x∈(c,b]时,f(x)是单调增函数,则f(x)在[a,b]上是单调增函数.
其中正确的命题序号是
分析:本题考查的是函数单调性的判断和证明问题,在解答时应注意进行单调性奇偶性的分析.如:①②可以通过定义理解,③可以通过据例说明,④可以通过数形结合画反例解决.
解答:解:f(x)=x2,满足f(2)>f(1),
但f(x)在R上不是增函数,是有增有减的,故①正确,
②函数f(x)=lg
(x≠0)的定义域为关于原点对称,且f(-x)=lg
=f(x)
∴函数f(x)是偶函数,其图象关于y轴对称;故②正确;
③令x=-1,则f(-1)=-2<2,故③错;
④如图,定义在[-4,4]上的函数f(x)在(-4,0)是增函数,
在[0,4]也是增函数,但f(x)在[-4,4]上不是减函数,故④错
故答案为①②.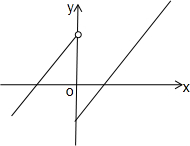
但f(x)在R上不是增函数,是有增有减的,故①正确,
②函数f(x)=lg
| x2+1 |
| |x| |
| (-x)2+1 |
| |-x| |
∴函数f(x)是偶函数,其图象关于y轴对称;故②正确;
③令x=-1,则f(-1)=-2<2,故③错;
④如图,定义在[-4,4]上的函数f(x)在(-4,0)是增函数,
在[0,4]也是增函数,但f(x)在[-4,4]上不是减函数,故④错
故答案为①②.

点评:此题是个基础题,本题考查的是函数单调性、奇偶性的判断和证明问题.在解答的过程当中充分体现了函数单调性的定义和数形结合的思想.值得同学们体会反思.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (文)如图,在单位正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:
(文)如图,在单位正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题: