题目内容
设曲线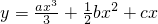 在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式
在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式 恒成立(a≠0).
恒成立(a≠0).
(1)求k(1)的值;
(2)求函数k(x)的表达式.
解:(1)解:k(x)=ax2+bx+c,∵ ,
,
∴ ,∴k(1)=1
,∴k(1)=1
(2)解:
∵k(x)≥x∴ ,
,
∴

即∴ ∴
∴
分析:(1)先求出函数k(x)的解析式,然后根据对一切实数x,不等式 恒成立,令x=1,即可求出k(1)的值;
恒成立,令x=1,即可求出k(1)的值;
(2)根据k(1)与k(-1)的值将b求出,将c用a表示,转化成 与,
与, 恒成立,利用判别式进行建立不等关系,解之即可.
恒成立,利用判别式进行建立不等关系,解之即可.
点评:本题主要考查了利用导数研究曲线上某点切线方程,函数恒成立问题等有关基础知识,考查运算求解能力,化归与转化思想,属于基础题.
 ,
,∴
 ,∴k(1)=1
,∴k(1)=1(2)解:

∵k(x)≥x∴
 ,
,∴


即∴
 ∴
∴
分析:(1)先求出函数k(x)的解析式,然后根据对一切实数x,不等式
 恒成立,令x=1,即可求出k(1)的值;
恒成立,令x=1,即可求出k(1)的值;(2)根据k(1)与k(-1)的值将b求出,将c用a表示,转化成
 与,
与, 恒成立,利用判别式进行建立不等关系,解之即可.
恒成立,利用判别式进行建立不等关系,解之即可.点评:本题主要考查了利用导数研究曲线上某点切线方程,函数恒成立问题等有关基础知识,考查运算求解能力,化归与转化思想,属于基础题.

练习册系列答案
相关题目

 在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式
在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式 恒成立(a≠0).
恒成立(a≠0).