题目内容
设曲线![]() 在点x处的切线斜率为k(x),且k(-1)=0.对一切实数x,不等式x≤k (x)≤
在点x处的切线斜率为k(x),且k(-1)=0.对一切实数x,不等式x≤k (x)≤![]() 恒成立(a≠0).
恒成立(a≠0).

(1)求k(1)的值;
(2)求函数k(x)的表达式;
(3)求证:![]() >
>![]()
答案:
解析:
解析:
|
(1)由 (2) 又 综上 (3) 要证原不等式式,即证 因为 所以 = 所以 本小问也可用数学归纳法求证.证明如下: 由 1.当 2D.假设当 当 由 所以 即当 综上得 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

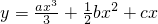 在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式
在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式 恒成立(a≠0).
恒成立(a≠0). 在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式
在点x处的切线斜率为k(x),且k(-1)=0,对一切实数x,不等式 恒成立(a≠0).
恒成立(a≠0).