题目内容
函数y=x-x
的图象大致为
- A.
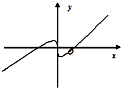
- B.
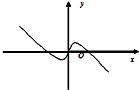
- C.
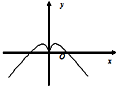
- D.
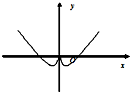
A
分析：利用y=x-x为奇函数可排除C，D，再利用x＞1时，y=x-x＞0再排除一个，即可得答案．
解答：令y=f（x）=x-x，
∵f（-x）=-x+
=-（x-）=-f（x），
∴y=f（x）=x-x为奇函数，
∴其图象关于原点成中心对称，故可排除C，D；
又x=1时，y=1-1=0，
当x＞1时，不妨令x=8，y=8-8=6＞0，可排除B，
故选A．
点评：本题考查函数的图象，着重考查函数的奇偶性与单调性，考查识图能力，属于中档题．
分析：利用y=x-x
为奇函数可排除C，D，再利用x＞1时，y=x-x＞0再排除一个，即可得答案．解答：令y=f（x）=x-x
，∵f（-x）=-x+
=-（x-）=-f（x），∴y=f（x）=x-x
为奇函数，∴其图象关于原点成中心对称，故可排除C，D；
又x=1时，y=1-1=0，
当x＞1时，不妨令x=8，y=8-8
=6＞0，可排除B，故选A．
点评：本题考查函数的图象，着重考查函数的奇偶性与单调性，考查识图能力，属于中档题．
练习册系列答案
相关题目
先作与函数y=lg
的图象关于原点对称的图象，再将所得图象向右平移2个单位得图象C1，又y=f（x）的图象C2与C1关于y=x对称，则y=f（x）的解析式是（ ）
| 1 |
| 2-x |
| A、y=10x |
| B、y=10x-2 |
| C、y=lgx |
| D、y=lg（x-2） |