题目内容
先作与函数y=lg
的图象关于原点对称的图象,再将所得图象向右平移2个单位得图象C1,又y=f(x)的图象C2与C1关于y=x对称,则y=f(x)的解析式是( )
| 1 |
| 2-x |
| A、y=10x |
| B、y=10x-2 |
| C、y=lgx |
| D、y=lg(x-2) |
分析:根据函数对称变换法则,函数y=lg
的图象关于原点对称的图象为y=-lg
=lg(x+2),再由平移变换法则,向右平移两个单位后得图象C1,则C1的解析式为y=lgx,由于y=f(x)的图象C2与C1关于y=x对称,则y=f(x)与y=lgx互为反函数,由反函数的定义,即可得到答案.
| 1 |
| 2-x |
| 1 |
| 2+x |
解答:解:函数y=lg
的图象关于原点对称的图象为y=-lg
=lg(x+2),
将y=lg(x+2)的图象向右平移两个单位后得图象C1的解析式为y=lgx
若y=f(x)的图象C2与C1关于y=x对称,
则y=f(x)与y=lgx互为反函数
故f(x)=10x
故选A
| 1 |
| 2-x |
| 1 |
| 2+x |
将y=lg(x+2)的图象向右平移两个单位后得图象C1的解析式为y=lgx
若y=f(x)的图象C2与C1关于y=x对称,
则y=f(x)与y=lgx互为反函数
故f(x)=10x
故选A
点评:互为反函数的两个函数图象关于线y=x对称,具体体现在:若f(x)的图象上有(a,b)点,则(b,a)点一定在其反函数的图象上;
如果两个函数图象关于 X轴对称,具体体现在:若f(x)的图象上有(a,b)点,则(a,-b)点一定在函数g(x)的图象上;
如果两个函数图象关于 Y轴对称,具体体现在:若f(x)的图象上有(a,b)点,则(-a,b)点一定在函数g(x)的图象上;
如果两个函数图象关于原点对称,具体体现在:若f(x)的图象上有(a,b)点,则(-a,-b)点一定在函数g(x)的图象上;
如果两个函数图象关于 X轴对称,具体体现在:若f(x)的图象上有(a,b)点,则(a,-b)点一定在函数g(x)的图象上;
如果两个函数图象关于 Y轴对称,具体体现在:若f(x)的图象上有(a,b)点,则(-a,b)点一定在函数g(x)的图象上;
如果两个函数图象关于原点对称,具体体现在:若f(x)的图象上有(a,b)点,则(-a,-b)点一定在函数g(x)的图象上;

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
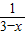 的图象关于原点对称的图象,再将所得图象向右平移3个单位得到图象C1.又y=f(x)的图象C2与C1关于y=x对称,则y=f(x)的解析式是 .
的图象关于原点对称的图象,再将所得图象向右平移3个单位得到图象C1.又y=f(x)的图象C2与C1关于y=x对称,则y=f(x)的解析式是 .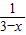 的图象关于原点对称的图象,再将所得图象向右平移3个单位得到图象C1.又y=f(x)的图象C2与C1关于y=x对称,则y=f(x)的解析式是 .
的图象关于原点对称的图象,再将所得图象向右平移3个单位得到图象C1.又y=f(x)的图象C2与C1关于y=x对称,则y=f(x)的解析式是 .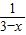 的图象关于原点对称的图象,再将所得图象向右平移3个单位得到图象C1.又y=f(x)的图象C2与C1关于y=x对称,则y=f(x)的解析式是 .
的图象关于原点对称的图象,再将所得图象向右平移3个单位得到图象C1.又y=f(x)的图象C2与C1关于y=x对称,则y=f(x)的解析式是 .