题目内容
已知数列{an}、{bn}中,对任何正整数n都有:a1bn+a2bn-1+a3bn-2+…+an-1b2+anb1=2n+1-n-2.
(1)若数列{an}是首项和公差都是1的等差数列,求证:数列{bn}是等比数列;
(2)若数列{bn}是等比数列,数列{an}是否是等差数列,若是,请求出通项公式;若不是,请说明理由;
(3)若数列{an}是等差数列,数列{bn}是等比数列,求证:![]() <
<![]() .
.
解:(1)依题意数列{an}的通项公式是an=n,
故等式即为bn+2bn-1+3bn-2+…+(n-1)b2+nb1=2n+1-n-2,
同时有bn-1+2bn-2+3bn-3+…+(n-2)b2+(n-1)b1=2n-n-1(n≥2),
两式相减可得bn+bn-1+…+b2+b1=2n-1,
可得数列{bn}的通项公式是bn=2n-1,
知数列{bn}是首项为1,公比为2的等比数列.
(2)设等比数列{bn}的首项为b,公比为q,则bn=bqn-1,从而有:
bqn-1a1+bqn-2a2+bqn-3a3+…+bqan-1+ban=2n+1-n-2.
又bqn-2a1+bqn-3a2+bqn-4a3+…+ban-1=2n-n-1(n≥2),
故(2n-n-1)q+ban=2n+1-n-2,
an=![]() ×2n+
×2n+![]() ×n+
×n+![]() ,
,
要使an+1-an是与n无关的常数,必须q=2,
即①当等比数列{bn}的公比q=2时,数列{an}是等差数列,其通项公式是an=![]() ;
;
②当等比数列{bn}的公比不是2时,数列{an}不是等差数列.
(3)证明:由(2)知anbn=n·2n,
![]() =
=![]() +…+
+…+![]() ,
,
![]() =
=![]() +…+
+…+![]() (n≥5)
(n≥5)
=![]() +
+![]() +
+![]() +
+![]() ×
×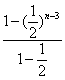
=![]() +
+![]() +
+![]() +
+![]() ×(
×(![]() )n-3
)n-3
=![]() ×(
×(![]() )n-3<
)n-3<![]() ×(
×(![]() )n-3<
)n-3<![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
