题目内容
已知k=
dx，直线y=kx+1交圆P：x2+y2=1于A，B两点，则|AB|= ．
| 1 |
| π |
| ∫ | 2 -2 |
| 4-x2 |
分析：先根据积分的几何意义求出k，然后根据直线与圆的位置关系即可求相交弦的弦长．
解答：解：根据积分的几何意义可知k=
dx=2，
∴直线方程为y=2x+1，
则圆心O到直线2x-y+1=0的距离d=
=
，
∴|AB|=2
=2
=2
=
．
故答案为：
．
| 1 |
| π |
| ∫ | 2 -2 |
| 4-x2 |
∴直线方程为y=2x+1，
则圆心O到直线2x-y+1=0的距离d=
| |1| | ||
|
| 1 | ||
|
∴|AB|=2
12-(
|
1-
|
|
4
| ||
| 5 |
故答案为：
4
| ||
| 5 |
点评：本题主要考查直线与圆的位置关系的应用，以及积分的几何意义，要求熟练掌握相应的计算公式，考查学生的计算能力．
练习册系列答案
相关题目
=(1,2), 
=(-2,1)，k,t为正实数，向量 
= 
+1)
=-k
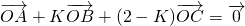（k为常数且0＜k＜2，O为坐标原点，S△BOC表示△BOC的面积）