题目内容
、已知向量 =(1,2),
=(1,2),  =(-2,1),k,t为正实数,向量
=(-2,1),k,t为正实数,向量  =
=  +(t
+(t +1)
+1) ,
,
 =-k
=-k +
+

(1)若 ⊥
⊥ ,求k的最小值;
,求k的最小值;
(2)是否存在正实数k、t,使 ∥
∥ ? 若存在,求出k的取值范围;若不存在,请说明理由.
? 若存在,求出k的取值范围;若不存在,请说明理由.
【答案】
(1)x=a+(t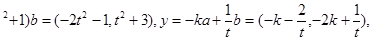
由x⊥y,得x·y=0,即(-2t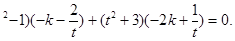
整理得k=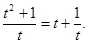 ∵t>0,∴k=
∵t>0,∴k=
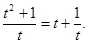 ≥2
≥2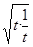 =2,当且仅当t=1时,k=2.
=2,当且仅当t=1时,k=2.
所以k的最小值为2.
(2)假设存在正实数k,t使x∥y,则(-2t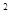 -1)(-2k+
-1)(-2k+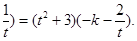 整理得tk(t
整理得tk(t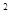 +1)+1=0.
+1)+1=0.
满足上述等式的正实数k、t不存在,所以不存在正实数k、t,使x∥y.
【解析】(1)利用 ⊥
⊥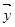 坐标化后建立关于k的方程,然后用t表示出k,从而得到k关于t的函数关系式,再考虑采用函数求最值的方法求k的最值.
坐标化后建立关于k的方程,然后用t表示出k,从而得到k关于t的函数关系式,再考虑采用函数求最值的方法求k的最值.
(II) 假设存在正实数k,t使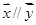 ,则(-2t
,则(-2t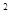 -1)(-2k+
-1)(-2k+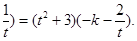 然后得到关于k,t的方程,判断此方程是否有解即可.
然后得到关于k,t的方程,判断此方程是否有解即可.
(1)x=a+(t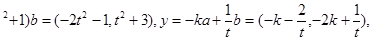
由x⊥y,得x·y=0,即(-2t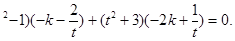
整理得k=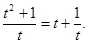 ∵t>0,∴k=
∵t>0,∴k=
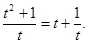 ≥2
≥2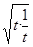 =2,当且仅当t=1时,k=2.
=2,当且仅当t=1时,k=2.
所以k的最小值为2.
(2)假设存在正实数k,t使x∥y,则(-2t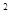 -1)(-2k+
-1)(-2k+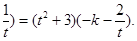 整理得tk(t
整理得tk(t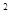 +1)+1=0.
+1)+1=0.
满足上述等式的正实数k、t不存在,所以不存在正实数k、t,使x∥y.

练习册系列答案
相关题目
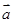 =
(1,2 ),
=
(1,2 ), 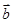 =
(2,-3 ),若向量
=
(2,-3 ),若向量 满足(
满足( ,
, )
B.(-
)
B.(- =(1,
=(1, ) ,
) , =(2,2)
,且
=(2,2)
,且 与
与 的值为
的值为