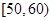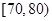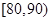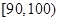题目内容
某中学为增强学生环保意识，举行了“环抱知识竞赛”，共有900名学生参加这次竞赛为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，请你根据尚未完成的频率分布表解答下列问题：| 分组 | 频数 | 频率 |
| [50，60） | 4 | 0.08 |
| [60，70） | ③ | 0.16 |
| [70，80） | 10 | ② |
| [80，90） | 16 | 0.32 |
| [90，100） | 0.24 | |
| 合计 | ① |
（Ⅱ）成绩在[70，90）分的学生约为多少人？
（Ⅲ）估计总体平均数．
分析：（I）根据频率的求法，频率=
，计算可得答案．
（II）频数分布直方图，清楚成绩在[70，90）分的学生不同区间内的频数，各组频数分布情况，求出各小组之间频数的和．
（III）欲估计总体平均数，根据平均数计算公式计算可得答案．
| 频数 |
| 数据总和 |
（II）频数分布直方图，清楚成绩在[70，90）分的学生不同区间内的频数，各组频数分布情况，求出各小组之间频数的和．
（III）欲估计总体平均数，根据平均数计算公式计算可得答案．
解答：
解：（Ⅰ）设抽取的样本为x名学生的成绩，
则由第一行中可知0.08=
，所以x=50∴①处的数值为50；
②处的数值为
=0.20；
③处的数值为50×0.16=8（4分）
（Ⅱ）成绩在[70，80）分的学生频率为0.2，成绩在[80.90）分的学生频率为0.32，
所以成绩在[70.90）分的学生频率为0.52，（6分）
由于有900名学生参加了这次竞赛，
所以成绩在[70.90）分的学生约为0.52×900=468（人）（8分）
（Ⅲ）利用组中值估计平均为55×0.08+65×0.16+75×0.20+85×0.32+95×0.24=79.8（12分）
解：（Ⅰ）设抽取的样本为x名学生的成绩，则由第一行中可知0.08=
| 4 |
| x |
②处的数值为
| 10 |
| 50 |
③处的数值为50×0.16=8（4分）
（Ⅱ）成绩在[70，80）分的学生频率为0.2，成绩在[80.90）分的学生频率为0.32，
所以成绩在[70.90）分的学生频率为0.52，（6分）
由于有900名学生参加了这次竞赛，
所以成绩在[70.90）分的学生约为0.52×900=468（人）（8分）
（Ⅲ）利用组中值估计平均为55×0.08+65×0.16+75×0.20+85×0.32+95×0.24=79.8（12分）
点评：本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
练习册系列答案
相关题目
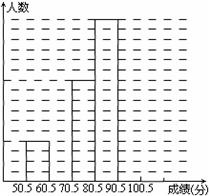为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表和频数分布直方图，解答下列问题：| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 | 0.16 | |
| 70.5～80.5 | 10 | |
| 80.5～90.5 | 16 | 0.32 |
| 90.5～100.5 | ||
| 合计 | 50 |
（Ⅱ）补全频数直方图；
（Ⅲ）学校决定成绩在75.5～85.5分的学生为二等奖，问该校获得二等奖的学生约为多少人？
某中学为增强学生环保意识，举行了“环抱知识竞成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，求①、②处的数值；
① . ② .
|
分组 |
频数 |
频率 |
|
|
4 |
0.08 |
|
|
8 |
0.16 |
|
|
10 |
② |
|
|
16 |
0.32 |
|
|
|
0.24 |
|
合计 |
① |
|
某中学为增强学生环保意识，举行了“环抱知识竞赛”，共有900名学生参加这次竞赛为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，请你根据尚未完成的频率分布表解答下列问题：
（Ⅰ）求①、②、③处的数值；
（Ⅱ）成绩在[70，90）分的学生约为多少人？
（Ⅲ）估计总体平均数．
| 分组 | 频数 | 频率 |
| [50，60） | 4 | 0.08 |
| [60，70） | ③ | 0.16 |
| [70，80） | 10 | ② |
| [80，90） | 16 | 0.32 |
| [90，100） | 0.24 | |
| 合计 | ① |
（Ⅱ）成绩在[70，90）分的学生约为多少人？
（Ⅲ）估计总体平均数．