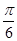题目内容
已知函数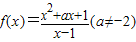 的图象关于点(b,1)对称.
的图象关于点(b,1)对称.(I)求a的值;
(II)求函数f(x)的单调区间;
(II)设函数g(x)=x3-3c2x-2c(c≤-1).若对任意x1∈[2,4],总存在x2∈[-1,0],使得f(x1)=g(x2)成立,求c的取值范围.
【答案】分析:(I)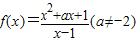 =x-1+
=x-1+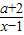 +a+2,由y=x+
+a+2,由y=x+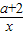 (a≠2)的图象有一个唯一的对称中心(0,0),f(x)的对称中心是(b,1),能求出a.
(a≠2)的图象有一个唯一的对称中心(0,0),f(x)的对称中心是(b,1),能求出a.
(II)由a=-1,b=1,知f(x)=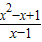 .
.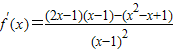 =
=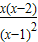 ,由此能求出函数f(x)的单调区间.
,由此能求出函数f(x)的单调区间.
(Ⅲ)由g(x)=x3-3c2x-2c(c≤-1),得g′(x)=3x2-3c2=3(x2-c2),由对任意x1∈[2,4],总存在x2∈[-1,0],使得f(x1)=g(x2)成立推导出-2c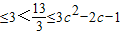 ,其中c≤-1.由此能求出c的取值范围.
,其中c≤-1.由此能求出c的取值范围.
解答:解:(I)∵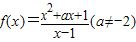
=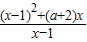
=x-1+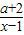 +a+2,
+a+2,
∵y=x+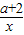 ,(a≠2)的图象有一个唯一的对称中心(0,0),
,(a≠2)的图象有一个唯一的对称中心(0,0),
∴f(x)有唯一一个对称中心(1,a+2),
∵f(x)的对称中心是(b,1),∴a=-1,b=1.
故a=-1.
(II)∵a=-1,b=1,∴f(x)=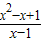 .
.
∴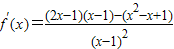 =
=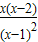 ,
,
列表讨论:
∴函数f(x)的增区间为(-∞,0)和(2,+∞),减区间为(0,1)和(1,2).
(Ⅲ)由g(x)=x3-3c2x-2c(c≤-1),得
g′(x)=3x2-3c2=3(x2-c2),
当x2∈[-1,0]时,g′(x2)≤0,
∴g(x2)∈[g(0),g(-1)].即g(x2)∈(-2c,-2c-1),
∵f(x)在[2,4]上是增区数,f(2)=3,f(4)=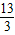 ,
,
∴ .
.
∵任意x1∈[2,4],总存在x2∈[-1,0],使得f(x1)=g(x2)成立,
∴-2c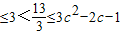 ,其中c≤-1.
,其中c≤-1.
∴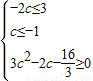 ,解得
,解得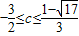 .
.
故c的取值范围是[- ,
,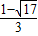 ].
].
点评:本题考查函数的对称中心的应用,考查函数的单调区间的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,注意导数性质、等价转化思想、分类讨论思想的合理运用.
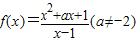 =x-1+
=x-1+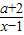 +a+2,由y=x+
+a+2,由y=x+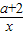 (a≠2)的图象有一个唯一的对称中心(0,0),f(x)的对称中心是(b,1),能求出a.
(a≠2)的图象有一个唯一的对称中心(0,0),f(x)的对称中心是(b,1),能求出a.(II)由a=-1,b=1,知f(x)=
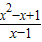 .
.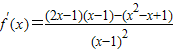 =
=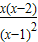 ,由此能求出函数f(x)的单调区间.
,由此能求出函数f(x)的单调区间.(Ⅲ)由g(x)=x3-3c2x-2c(c≤-1),得g′(x)=3x2-3c2=3(x2-c2),由对任意x1∈[2,4],总存在x2∈[-1,0],使得f(x1)=g(x2)成立推导出-2c
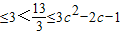 ,其中c≤-1.由此能求出c的取值范围.
,其中c≤-1.由此能求出c的取值范围.解答:解:(I)∵
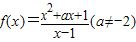
=
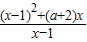
=x-1+
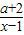 +a+2,
+a+2,∵y=x+
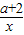 ,(a≠2)的图象有一个唯一的对称中心(0,0),
,(a≠2)的图象有一个唯一的对称中心(0,0),∴f(x)有唯一一个对称中心(1,a+2),
∵f(x)的对称中心是(b,1),∴a=-1,b=1.
故a=-1.
(II)∵a=-1,b=1,∴f(x)=
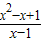 .
.∴
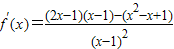 =
=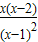 ,
,列表讨论:
| x | (-∞,0) | 0 | (0,1) | 1 | (1,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 不存在 | - | + | |
| f(x) | ↑ | -1 | ↓ | 不存在 | ↓ | 3 | ↑ |
(Ⅲ)由g(x)=x3-3c2x-2c(c≤-1),得
g′(x)=3x2-3c2=3(x2-c2),
当x2∈[-1,0]时,g′(x2)≤0,
∴g(x2)∈[g(0),g(-1)].即g(x2)∈(-2c,-2c-1),
∵f(x)在[2,4]上是增区数,f(2)=3,f(4)=
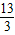 ,
,∴
 .
.∵任意x1∈[2,4],总存在x2∈[-1,0],使得f(x1)=g(x2)成立,
∴-2c
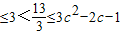 ,其中c≤-1.
,其中c≤-1.∴
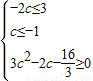 ,解得
,解得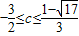 .
.故c的取值范围是[-
 ,
,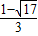 ].
].点评:本题考查函数的对称中心的应用,考查函数的单调区间的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,注意导数性质、等价转化思想、分类讨论思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
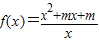 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;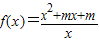 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;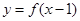 的图象关于点
的图象关于点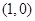 对称,且当
对称,且当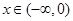 时,
时,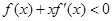 成立(其中
成立(其中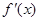 是
是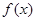 的导函数),若
的导函数),若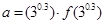 ,
,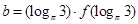 ,
, ,则
,则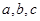 的大小关系是( )
的大小关系是( )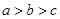 B.
B.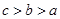 C.
C. 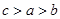 D.
D.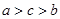
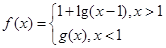 的图象关于点
的图象关于点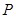 对称,且函数
对称,且函数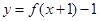 为奇函数,则下列结论:(1)点
为奇函数,则下列结论:(1)点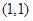 ;(2)当
;(2)当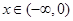 时,
时,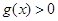 恒成立;(3)关于
恒成立;(3)关于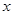 的方程
的方程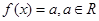 有且只有两个实根。其中正确结论的题号为( )
有且只有两个实根。其中正确结论的题号为( )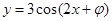 的图象关于点
的图象关于点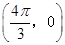 中心对称,则
中心对称,则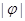 的最小值为
的最小值为 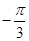 B.
B.
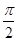 C.
C.
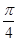 D.
D.