题目内容
在 中,角
中,角 ,
, ,
, 的对边是
的对边是 ,
, ,
, ,且
,且 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求 面积的最大值.
面积的最大值.
(Ⅰ)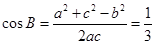 ;(Ⅱ)
;(Ⅱ) 的面积的最大值为
的面积的最大值为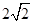 .
.
解析试题分析:(Ⅰ)解法一:
由 及正弦定理得
及正弦定理得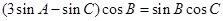 , (2分)
, (2分)
即 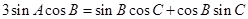 ,
,
所以 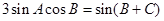 , (4分)
, (4分)
由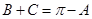 及诱导公式得
及诱导公式得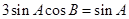 , (6分)
, (6分)
又 中
中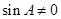 ,得
,得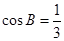 . (7分)
. (7分)
解法二:
由 及余弦定理得
及余弦定理得 (3分)
(3分)
化简得: 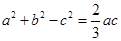 (5分)
(5分)
所以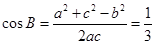 (7分)
(7分)
(Ⅱ)由(Ⅰ)知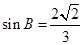 (8分)
(8分)
由 及余弦定理得
及余弦定理得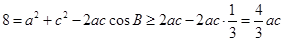 (11分)
(11分)
即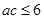 (当且仅当
(当且仅当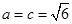 时取到等号)
时取到等号)
所以 的面积为
的面积为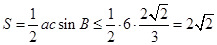
所以 的面积的最大值为
的面积的最大值为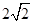 . (14分
. (14分
考点:两角和与差的三角函数,正弦定理、余弦定理的应用,三角形面积。
点评:中档题,三角形中的问题,往往利用两角和与差的三角函数公式进行化简,利用正弦定理、余弦定理建立边角关系。本题综合性较强,综合考查两角和与差的三角函数,正弦定理、余弦定理的应用,三角形面积。

练习册系列答案
相关题目
 ,
,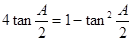 .
.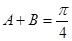 ;
;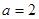 ,求c和ΔABC的面积.
,求c和ΔABC的面积. .
. 的单调递增区间;
的单调递增区间;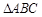 中,三内角
中,三内角 的对边分别为
的对边分别为 ,已知
,已知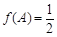 ,
,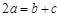 ,
, .求
.求 的值.
的值. 的三个内角且向量
的三个内角且向量 与
与 共线.
共线. 的对边分别是
的对边分别是 ,且满足
,且满足 ,试判断
,试判断
 的形状.
的形状.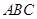 中,
中,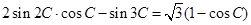 .
.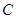 的大小;
的大小; ,且
,且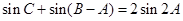 ,求
,求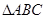 的面积.
的面积.  海里的速度向正北方向航行,
海里的速度向正北方向航行,
 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,c.已知
,c.已知 .
.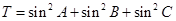 ,求T的取值范围.
,求T的取值范围.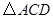 是等边三角形,
是等边三角形,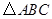 是等腰直角三角形,
是等腰直角三角形, ,
,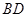 交
交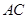 于
于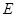 ,
,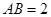 .
.
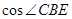 的值;
的值;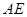 .
. 中,角
中,角 的对边分别是
的对边分别是 ,且
,且
 的大小:
的大小: 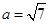 ,且
,且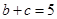 ,求
,求