题目内容
圆锥的轴截面是等腰直角三角形，且圆锥的底面积为10，则它的侧面积为
- A.10
- B.10π
- C.5
- D.5π
A
分析：求出圆锥的底面直的底面半径，然后求出圆锥的母线，即可求解圆锥的侧面积．
解答：∵圆锥的轴截面是等腰直角三角形，设圆锥的底面半径为r，
圆锥的轴截面是等腰直角三角形，
∴圆锥的母线长为r，
∵圆锥的底面积为10．
∴圆锥的底面半径为：r=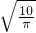
，圆锥的母线长为
，
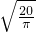底面周长为：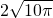
．
圆锥的侧面积为：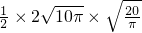
=10．
故选A．
点评：考查圆锥的计算；得到圆锥的底面半径是解决本题的突破点；注意圆锥的侧面积=
×底面周长×母线长的应用．
分析：求出圆锥的底面直的底面半径，然后求出圆锥的母线，即可求解圆锥的侧面积．
解答：∵圆锥的轴截面是等腰直角三角形，设圆锥的底面半径为r，
圆锥的轴截面是等腰直角三角形，
∴圆锥的母线长为
r，∵圆锥的底面积为10．
∴圆锥的底面半径为：r=
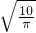，圆锥的母线长为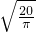，底面周长为：
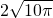．圆锥的侧面积为：
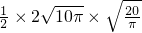=10．故选A．
点评：考查圆锥的计算；得到圆锥的底面半径是解决本题的突破点；注意圆锥的侧面积=
×底面周长×母线长的应用． 
练习册系列答案
相关题目
求答下列三小题：
)，问能否确定θ，使得三棱锥C—SOD的体积最大？若能，求出体积的最大值和对应的θ；若不能，请说明理由．
，垂足为B，
，垂足为H，且PA=4，C为PA的中点，则当三棱锥O－HPC的体积最大时，OB的长是（ ）
B. 
C. 
D. 
，垂足为B，
，垂足为H，且PA=4，C为PA的中点，则当三棱锥O－HPC的体积最大时，OB的长是（ ）
B. 
C. 
D. 