题目内容
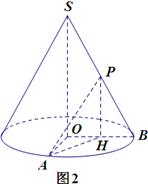
已知:如图,圆锥SO的轴截面是等腰直角三角形,其母线长为4a,A为底面圆周上一点,B是底面圆内一点,且OB⊥AB,C是SA的中点,D是O在SB上的射影.

(Ⅰ)求证:OD⊥平面SAB;
(Ⅱ)设平面SOA和平面SAB所成的二面角为θ(0<θ< ),问能否确定θ,使得三棱锥C—SOD的体积最大?若能,求出体积的最大值和对应的θ;若不能,请说明理由.
),问能否确定θ,使得三棱锥C—SOD的体积最大?若能,求出体积的最大值和对应的θ;若不能,请说明理由.
答案:
解析:
解析:
|
(1)证明 由SO垂直于⊙O所在平面,AB在⊙O内,可得AB⊥SO. ∵AB⊥SO,AB⊥OB,OB 而OD ∴OD⊥AB. 又OD⊥SB,SB ∴OD⊥平面SAB. (2)解 由圆锥SO的轴截面是等腰直角三角形,得OS=OA. 又C是SA的中点,∴OC⊥SA. 由OD⊥平面SAB,OC⊥SA,得DC⊥SA,∠OCD是平面SOA和平面SAB所成的二面角的平面角,则∠OCD=θ. 又∵OC⊥SA,DC⊥SA,OC ∴SA⊥平面COD. 由题意知:△COD是Rt△,且 故得: = 当且仅当OD=CD=
即存在θ= |

练习册系列答案
相关题目
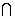 OS=O,∴AB⊥平面SOB.
OS=O,∴AB⊥平面SOB. 平面SOB,
平面SOB,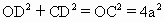 .
.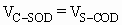 =
=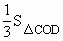 ·SC=
·SC= OD·CD≤
OD·CD≤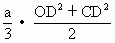
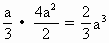 .
.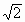 a时,
a时,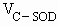 最大.
最大.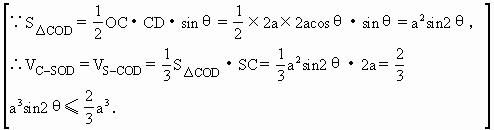
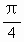 ,使得三棱锥C-SOD的体积最大,其体积的最大值为
,使得三棱锥C-SOD的体积最大,其体积的最大值为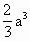 .
. 如图,已知圆锥的底面半径为r=10,点Q为半圆弧
如图,已知圆锥的底面半径为r=10,点Q为半圆弧

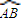 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为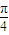 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积.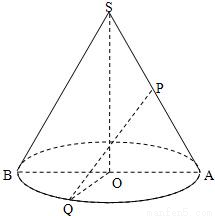
 的侧面积为
的侧面积为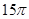 ,底面半径
,底面半径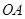 和
和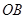 互相垂直,且
互相垂直,且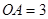 ,
, 是母线
是母线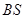 的中点.
的中点.
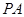 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示). 得
得 ,故
,故
 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.  (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角. 平面OAB,
平面OAB, PH
PH OAH中,由OA
OAH中,由OA ;
; 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan