题目内容
在直三棱柱ABC－A1B1C1中，∠ACB＝90°，BC＝CC1＝a，AC＝2a．
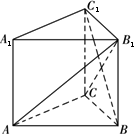
(Ⅰ)求证：AB1⊥BC1；
(Ⅱ)求二面角B－AB1－C的大小；
(Ⅲ)求点A1到平面AB1C的距离．
答案：
解析：
解析：
|
解：(Ⅰ)证明：∵平面BCC1B1是正方形，∴BC1⊥B1C 又∵B1C是AB1在平面BCC1B1的的射影 ∴由三垂线定理的：AB1⊥BC1 (4分) (Ⅱ)过点C做CH⊥AB于点H，则CH⊥平面ABB1 过点H做HD⊥AB1于点D，连接CD，则CD⊥AB1
|
练习册系列答案
习题精选系列答案
相关题目
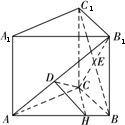
如图，在直三棱柱ABC-A1B1C1中，已知AB=AC，F为BB1上一点，BF=BC=2，FB1=1，D为BC中点，E为线段AD上不同于点A、D的任意一点．
如图，在直三棱柱ABC-A1B1C1中，底面ABC是等腰直角三角形，斜边
在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=BC=AA1=1，D、E分别为棱AB、BC的中点，M为棱AA1上的点．
如图，在直三棱柱ABC-A1B1C1中，AC=BC=AA1=2，∠ACB=90°，D、E分别为AC、AA1的中点．点F为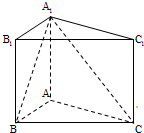
如图，在直三棱柱ABC-A1B1C1中，AB=1，