题目内容
19.已知数列{an}的前n项和为Sn,a1=1,2an+1=Sn+2.(1)求a2,a3,并求数列通项公式an;
(2)求Sn;
(3)求{$\frac{1}{{a}_{n}}$}的前n项和Tn.
分析 (1)由条件,将n换成n-1,两式相减,由等比数列的定义和通项,可得数列的通项公式;
(2)运用已知2an+1=Sn+2,即可解得前n项和为Sn;
(3)由等比数列的求和公式,计算即可得到前n项和Tn.
解答 解:(1)a1=1,2an+1=Sn+2,
即有2an=Sn-1+2,n>1.
相减可得,2an+1-2an=an,
即为an+1=$\frac{3}{2}$an,
由2a2=a1+2,可得a2=$\frac{3}{2}$,
2a3=a1+a2+2,可得a3=$\frac{9}{4}$,
由等比数列的通项公式可得an=$\frac{3}{2}$•($\frac{3}{2}$)n-2,n>1.
即有an=($\frac{3}{2}$)n-1,对n=1也成立,
则数列的通项公式为an=($\frac{3}{2}$)n-1;
(2)由2an+1=Sn+2,可得
Sn=2an+1-2=2•($\frac{3}{2}$)n-2;
(3)由$\frac{1}{{a}_{n}}$=($\frac{2}{3}$)n-1;
则{$\frac{1}{{a}_{n}}$}的前n项和Tn=$\frac{1-(\frac{2}{3})^{n}}{1-\frac{2}{3}}$=3-3•($\frac{2}{3}$)n.
点评 本题考查数列的通项和求和之间的关系,考查等比数列的通项公式和求和公式的运用,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
9.下列函数中,是偶函数且图象关于x=$\frac{π}{2}$对称的函数是( )
| A. | y=sin2x | B. | y=cosx | C. | y=sin($\frac{π}{2}$-2x) | D. | y=tanx |
14.已知非零向量$\overrightarrow{AB}$与$\overrightarrow{AC}$满足($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$)•$\overrightarrow{BC}$=0,且$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$=$\frac{1}{4}$,则△ABC为( )
| A. | 三边均不相等的三角形 | B. | 直角三角形 | ||
| C. | 等腰非等边三角形 | D. | 等边三角形 |
13.若a<b<0,则下列结论一定正确的是( )
| A. | $\frac{a+b}{2}$>$\sqrt{ab}$ | B. | $\frac{1}{|a|}$>$\frac{1}{|b|}$ | C. | ac2<bc2 | D. | (a+$\frac{1}{b}$)2>(b+$\frac{1}{a}$)2 |
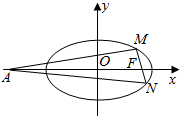 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).