题目内容
设平面向量
=(-2,1),
=(λ,-1),若
与
的夹角为钝角,则λ的取值范围是( )
| a |
| b |
| a |
| b |
分析:两个向量在不共线的条件下,夹角为钝角的充要条件是它们的数量积小于零.由此列出不等式组,再解出这个不等式组,所得解集即为实数λ的取值范围.
解答:解:由题意,可得
•
=-2•λ+1×(-1)<0,且λ-(-2)×(-1)≠0,
∴λ>-
,且 λ≠2,
故实数x的取值范围为 (-
,2)∪(2,+∞),
故选A
| a |
| b |
∴λ>-
| 1 |
| 2 |
故实数x的取值范围为 (-
| 1 |
| 2 |
故选A
点评:本题考查了向量的数量积、两个向量共线关系等知识点,属于基础题.在解决两个向量夹角为钝角(锐角)的问题时,千万要注意两个向量不能共线,否则会有遗漏而致错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
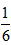 ),且a∥b,求sin2α的值。
),且a∥b,求sin2α的值。