题目内容
设平面向量
=(-2,1),
=(1,λ),若
与
的夹角为钝角,则λ的取值范围是
| a |
| b |
| a |
| b |
(-∞,-
)∪(-
,2)
| 1 |
| 2 |
| 1 |
| 2 |
(-∞,-
)∪(-
,2)
.| 1 |
| 2 |
| 1 |
| 2 |
分析:判断出向量的夹角为钝角的充要条件是数量积为负且不反向,利用向量的数量积公式及向量共线的充要条件求出λ的范围.
解答:解:
,
夹角为钝角
∴
•
<0且不反向
即-2+λ<0解得λ<2
当两向量反向时,存在m<0使
=m
即(-2,1)=(m,mλ)
解得λ=-
所以 λ的取值范围 (-∞,-
)∪(-
,2)
故答案为(-∞,-
)∪(-
,2).
| a |
| b |
∴
| a |
| b |
即-2+λ<0解得λ<2
当两向量反向时,存在m<0使
| a |
| b |
即(-2,1)=(m,mλ)
解得λ=-
| 1 |
| 2 |
所以 λ的取值范围 (-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查向量夹角的范围问题.通过向量数量积公式变形可以解决.但要注意数量积为负,夹角包括钝角和平角两类.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
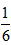 ),且a∥b,求sin2α的值。
),且a∥b,求sin2α的值。