题目内容
关于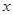 的方程
的方程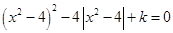 ,给出下列四个命题:
,给出下列四个命题:
①存在实数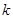 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数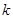 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数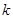 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数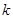 ,使得方程恰有8个不同的实根.
,使得方程恰有8个不同的实根.
其中假命题的个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】
A
【解析】关于x的方程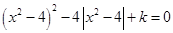 可化为
可化为 (1)或
(1)或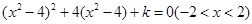 (2).
(2).
当k=4时,方程(1)的解为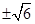 ,方程(2)有两个不同的实根
,方程(2)有两个不同的实根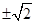 ,原方程恰有4个不同的实根.
,原方程恰有4个不同的实根.
当k=-12时,方程(1)的解为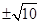 ,方程(2)无解,原方程恰有2个不同的实根,
,方程(2)无解,原方程恰有2个不同的实根,
当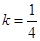 时,方程(1)有两个不同的实根
时,方程(1)有两个不同的实根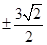 ,方程(2)有两个不同的实根
,方程(2)有两个不同的实根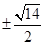 ,即原方程恰有4个不同的实根.
,即原方程恰有4个不同的实根.
当k=0时,方程(1)的解为 ,方程(2)的解为
,方程(2)的解为 ,原方程恰有5个不同的实根,
,原方程恰有5个不同的实根,
当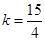 时,方程(1)的解为
时,方程(1)的解为 ,方程(2)的解为
,方程(2)的解为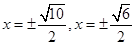 ,即原方程恰有8个不同的实根.
,即原方程恰有8个不同的实根.

练习册系列答案
相关题目
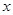 的方程
的方程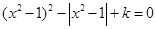 ,给出下列四个命题:
,给出下列四个命题: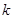 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;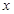 的方程
的方程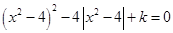 ,给出下列四个命题:
,给出下列四个命题:
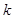 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;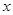 的方程
的方程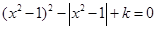 ,给出下列四个命题:
,给出下列四个命题: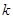 ,使得方程恰有2个不同实根;
,使得方程恰有2个不同实根;