题目内容
关于![]() 的方程
的方程![]() ,给出下列四个命题:
,给出下列四个命题:
①存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数![]() ,使得方程恰有8个不同的实根.
,使得方程恰有8个不同的实根.
其中假命题的个数是 ( )
A.0 B.1 C.2 D.3
B
解析:
据题意可令![]()
![]() ①,则方程化为
①,则方程化为![]() ②,作出函数
②,作出函数![]() 的图象,结合函数的图象可知:(1)当t=0或t>1时方程①有2个不等的根;(2)当0<t<1时方程①有4个根;(3)当t=1时,方程①有3个根.
的图象,结合函数的图象可知:(1)当t=0或t>1时方程①有2个不等的根;(2)当0<t<1时方程①有4个根;(3)当t=1时,方程①有3个根.
故当t=0时,代入方程②,解得k=0此时方程②有两个不等根t=0或t=1,故此时原方程有5个根;当方程②有两个不等正根时,即![]() 此时方程②有两根且均小于1大于0,故相应的满足方程
此时方程②有两根且均小于1大于0,故相应的满足方程![]() 的解有8个,即原方程的解有8个;当
的解有8个,即原方程的解有8个;当![]() 时,方程②有两个相等正根t=
时,方程②有两个相等正根t=![]() ,相应的原方程的解有4个;故选B.
,相应的原方程的解有4个;故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
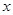 的方程
的方程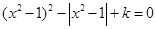 ,给出下列四个命题:
,给出下列四个命题: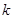 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;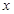 的方程
的方程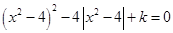 ,给出下列四个命题:
,给出下列四个命题:
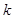 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;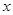 的方程
的方程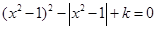 ,给出下列四个命题:
,给出下列四个命题: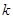 ,使得方程恰有2个不同实根;
,使得方程恰有2个不同实根;