题目内容
1.若cos2α=a,求sin4α-cos4α的值.分析 利用三角函数的倍角公式进行化简即可.
解答 解:sin4α-cos4α=(sin2α-cos2α)(sin2α+cos2α)=sin2α-cos2α=-cos2α=-a.
点评 本题主要考查三角函数的化简和求值,利用平方差公式结合二倍角公式是解决本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
16.一个平面内的8个点,若只有4个点共圆,其余任何4点不共圆,那么这8个点最多确定的圆的个数为( )
| A. | ${C}_{4}^{3}$•${C}_{4}^{4}$ | B. | ${C}_{8}^{3}$-${C}_{4}^{3}$ | C. | 2${C}_{4}^{1}$•${C}_{4}^{2}$+${C}_{4}^{3}$ | D. | ${C}_{8}^{3}$-${C}_{4}^{3}$+1 |
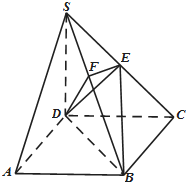 如图,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥底面ABCD,SD=DC=2,E是SC的中点,作EF⊥SB交SB于F.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥底面ABCD,SD=DC=2,E是SC的中点,作EF⊥SB交SB于F. 如图,抛物线C1:y2=4x的焦准距(焦点到准线的距离)与椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$
如图,抛物线C1:y2=4x的焦准距(焦点到准线的距离)与椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$