题目内容
正三棱锥S-ABC的高为2,侧棱与底面所成的角为45°,则其内切球的半径R=分析:根据题意和正三棱锥的结构特征,求出底面的边长和侧面的高,再由三棱锥的体积相等列出方程,求出内切球的半径.
解答:解:如图:设SO⊥底面ABC,则O是正三角形的中心,取AB的中点D,连接SD、OD、OB,
即SD⊥AB,OD⊥AB,

由题意知,SO=2,∠SDO=45°,则SD=2
,
在RT△ODB中,OD=2,∠OBD=30°,BD=2
,则AB=4
,
设内切球的半径R,由三棱锥的体积相等得,
×
×4
×4
×
×2=
×
×4
×4
×
×R+3×
×
×4
×2
×R
解得,R=2(
-1),
故答案为:2(
-1).
即SD⊥AB,OD⊥AB,

由题意知,SO=2,∠SDO=45°,则SD=2
| 2 |
在RT△ODB中,OD=2,∠OBD=30°,BD=2
| 3 |
| 3 |
设内切球的半径R,由三棱锥的体积相等得,
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
解得,R=2(
| 2 |
故答案为:2(
| 2 |
点评:本题考查了正三棱锥的结构特征和体积相等法的应用,考查了空间想象能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知正三棱锥S-ABC的三条侧棱两两互相垂直,且SA=2
,则正三棱锥S-ABC的外接球的表面积是( )
| 3 |
| A、12π | B、32π |
| C、36π | D、48π |
 如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.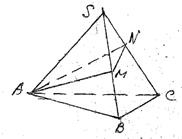 正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
 如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为
如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为