题目内容
19.一扇形如图所示,OA⊥OB,OA=OB=1,P为$\widehat{AB}$上一动A点,则$\overrightarrow{AP}$$•\overrightarrow{BP}+|\overrightarrow{OA}+\overrightarrow{OB}|$的取值范围为[1,$\sqrt{2}$].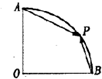
分析 分别以OB、OA所在直线为x轴、y轴建立平面直角坐标系,设出P的坐标,把$\overrightarrow{AP}$$•\overrightarrow{BP}+|\overrightarrow{OA}+\overrightarrow{OB}|$用含有P的坐标表示,然后利用$(x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}$的几何意义求解.
解答 解:建立如图所示平面直角坐标系,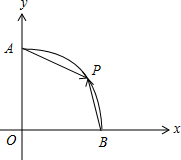
则B(1,0),A(0,1),设P(x,y)(0≤x≤1),
则$\overrightarrow{AP}=(x,y-1),\overrightarrow{BP}=(x-1,y)$,$|\overrightarrow{OA}+\overrightarrow{OB}|=\sqrt{2}$,
∴$\overrightarrow{AP}$$•\overrightarrow{BP}+|\overrightarrow{OA}+\overrightarrow{OB}|$=x(x-1)+y(y-1)+$\sqrt{2}$
=${x}^{2}+{y}^{2}-x-y+\sqrt{2}$=$(x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}-\frac{1}{2}+\sqrt{2}$.
$(x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}$的几何意义为扇形弧上的点与点M($\frac{1}{2},\frac{1}{2}$)距离的平方,
∴当点P位于OM的连线与扇形弧交点时,$(x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}$的值最小为$(1-\frac{\sqrt{2}}{2})^{2}=\frac{3}{2}-\sqrt{2}$,
此时$\overrightarrow{AP}$$•\overrightarrow{BP}+|\overrightarrow{OA}+\overrightarrow{OB}|$的最小值为$\frac{3}{2}-\sqrt{2}-\frac{1}{2}+\sqrt{2}=1$;
当点P位于A(或B)时,$(x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}$的值最大为$(1-\frac{1}{2})^{2}+(0-\frac{1}{2})^{2}=\frac{1}{2}$,
此时$\overrightarrow{AP}$$•\overrightarrow{BP}+|\overrightarrow{OA}+\overrightarrow{OB}|$的最大值为$\frac{1}{2}-\frac{1}{2}+\sqrt{2}=\sqrt{2}$.
故答案为:[1,$\sqrt{2}$].
点评 本题考查平面向量的数量积运算,考查了向量的坐标运算,考查数形结合的解题思想方法,是中档题.

| A. | 2x+y-1=0 | B. | 2x+y+1=0 | C. | 2x-y-1=0 | D. | 2x-y+1=0 |