题目内容
已知命题p：a＞0＞b，命题q：|a+b|＜|a|+|b|，则命题p是q的（ ）A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【答案】分析：由a＞0＞b，可得|a+b|＜|a|+|b|，由|a+b|＜|a|+|b|，可得ab＜0，从而可判断
解答：解：∵若a＞0＞b，则|a+b|＜|a|+|b|，
若|a+b|＜|a|+|b|，则ab＜0?a＜0＜b或b＜0＜a
命题p是q的充分不必要条件
故选A
点评：本题主要考查了充分、必要条件的判断，解题的关键是准确利用绝对值不等式的性质
解答：解：∵若a＞0＞b，则|a+b|＜|a|+|b|，
若|a+b|＜|a|+|b|，则ab＜0?a＜0＜b或b＜0＜a
命题p是q的充分不必要条件
故选A
点评：本题主要考查了充分、必要条件的判断，解题的关键是准确利用绝对值不等式的性质
练习册系列答案
阅读快车系列答案
相关题目
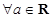,且a>0,有
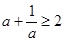,命题q: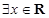
,
,则下列判断正确的是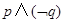
是真命题 D．
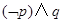是真命题