题目内容
已知命题
p:“a>0,b>0”是“方程ax2+by2=1”表示椭圆的充要条件;
q:在复平面内,复数
所表示的点在第二象限;
r:直线l⊥平面α,平面α∥平面β,则直线l⊥平面β;
s:同时抛掷两枚硬币,出现一正一反的概率为
,
则下列复合命题中正确的是( )
p:“a>0,b>0”是“方程ax2+by2=1”表示椭圆的充要条件;
q:在复平面内,复数
| 1-i |
| 1+i |
r:直线l⊥平面α,平面α∥平面β,则直线l⊥平面β;
s:同时抛掷两枚硬币,出现一正一反的概率为
| 1 |
| 3 |
则下列复合命题中正确的是( )
| A、p且q | B、r或s |
| C、非r | D、q或s |
分析:p.根据椭圆的方程和定义进行判断.q.根据复数的几何意义进行判断.r.根据线面垂直的判定定理进行判断.s.根据古典概率的概率公式进行判断.然后根据复合命题之间的关系进行判断.
解答:解:p.当a=b>0时,此时方程表示为圆,∴p为假命题.
q.
=
=
=-2i,对应的点为(0,-2)在y轴上,∴q为假命题.
r.根据线面垂直的性质可知,当l⊥平面α,平面α∥平面β,则直线l⊥平面β成立,∴r为真命题.
s.同时抛掷两枚硬币,则有4个结果,出现一正一反的有2个结果,∴出现一正一反的概率为
=
,∴s为假命题.
∴p且q为假命题,r或s为真命题,非r为假命题,q或s为假命题.
故选:B.
q.
| 1-i |
| 1+i |
| (1-i)2 |
| (1-i)(1+i) |
| 1-2i+i2 |
| 2 |
r.根据线面垂直的性质可知,当l⊥平面α,平面α∥平面β,则直线l⊥平面β成立,∴r为真命题.
s.同时抛掷两枚硬币,则有4个结果,出现一正一反的有2个结果,∴出现一正一反的概率为
| 2 |
| 4 |
| 1 |
| 2 |
∴p且q为假命题,r或s为真命题,非r为假命题,q或s为假命题.
故选:B.
点评:本题主要考查复合命题与简单命题之间的关系,利用条件分别进行判断是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
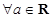 ,且a>0,有
,且a>0,有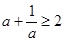 ,命题q:
,命题q: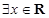 ,
, ,则下列判断正确的是
,则下列判断正确的是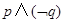 是真命题 D.
是真命题 D.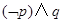 是真命题
是真命题