题目内容
已知椭圆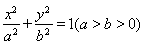 的右焦点为F2(1,0),点
的右焦点为F2(1,0),点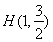 在椭圆上.
在椭圆上.

(1)求椭圆方程;
(2)点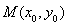 在圆
在圆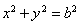 上,M在第一象限,过M作圆
上,M在第一象限,过M作圆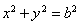 的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由.
的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由.
【答案】
(1)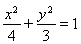 ;(2)|F2P|+|F2Q|+|PQ|是定值,等于4.
;(2)|F2P|+|F2Q|+|PQ|是定值,等于4.
【解析】
试题分析:(1)右焦点为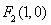 ,左焦点为
,左焦点为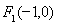 ,点
,点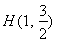 在椭圆上,由椭圆的定义可得
在椭圆上,由椭圆的定义可得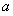 ,再由
,再由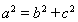 可得
可得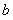 ,从而得椭圆的方程. (2)由于PQ与圆切于点M,故用切线长公式求出PM、MQ,二者相加求得PQ.求
,从而得椭圆的方程. (2)由于PQ与圆切于点M,故用切线长公式求出PM、MQ,二者相加求得PQ.求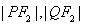 ,可用两点间的距离公式,将它们相加,若是一个与点
,可用两点间的距离公式,将它们相加,若是一个与点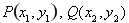 的坐标无关的常数,则是一个定值;否则,则不是定值.
的坐标无关的常数,则是一个定值;否则,则不是定值.
试题解析:(1) 右焦点为
右焦点为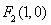 ,
,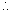
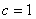
左焦点为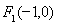 ,点
,点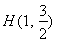 在椭圆上
在椭圆上
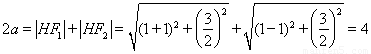
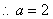 ,
,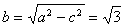
所以椭圆方程为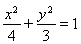 5分
5分
(2)设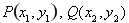 ,
,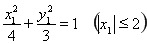
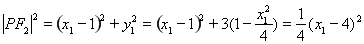
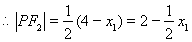 8分
8分
连接OM,OP,由相切条件知:
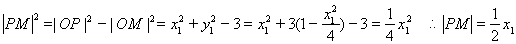
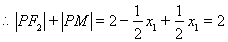 11分
11分
同理可求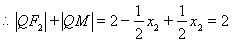
所以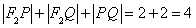 为定值。 13分
为定值。 13分
考点:1、椭圆的方程;2、直线与圆锥曲线;3、圆的切线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.  ,试用
,试用 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C