题目内容
若一个正三棱柱的高为1,体积为2
,则一条侧棱到与它相对的面之间的距离为( )
| 3 |
分析:根据体积公式V=Sh可得底面积为S=
=2
,再设底面三角形的边长为a,从而有
a2=2
,求出底面三角形的边长,再根据侧棱到相对面的距离底面三角形的高即可得出答案.
| V |
| h |
| 3 |
| ||
| 4 |
| 3 |
解答:解:由体积公式V=Sh可得底面积为S=
=2
,
若设底面三角形的边长为a,
则有
a2=2
,所以a=2
,
故侧棱到相对面的距离为
a=
.
故选D.
| V |
| h |
| 3 |
若设底面三角形的边长为a,
则有
| ||
| 4 |
| 3 |
| 2 |
故侧棱到相对面的距离为
| ||
| 2 |
| 6 |
故选D.
点评:本题考查棱柱的体积的计算方法,考查学生空间想象能力,是基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若一个正三棱柱的三视图如图所示,则这个正三棱柱的高和底面边长分别为( )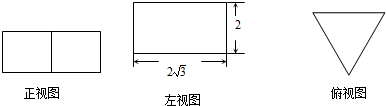

A、2,2
| ||
B、2
| ||
| C、4,2 | ||
| D、2,4 |
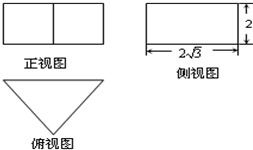 若一个正三棱柱的三视图如图所示,则这个正三棱柱的高和底面边长分别为
若一个正三棱柱的三视图如图所示,则这个正三棱柱的高和底面边长分别为

 B、
B、
 D、
D、