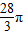题目内容
若一个正三棱柱的底面边长为2，高为2，其顶点都在一个球面上，则该球的表面积为（ ）
分析：根据正三棱柱的对称性，它的外接球的球心在上下底面中心连线段的中点．再由正三角形的性质和勾股定理，结合题中数据算出外接球半径R=
，用球表面积公式即可算出该球的表面积．
| ||
| 3 |
解答：解：设三棱柱ABC-A'B'C'的上、下底面的中心分别为O、O'，
根据图形的对称性，可得外接球的球心在线段OO'中点O1，
∵OA=
AB=
，OO1=
AA'=1
∴O1A=
=
=
因此，正三棱柱的外接球半径R=
，可得该球的表面积为S=4πR2=
π
故选：C
根据图形的对称性，可得外接球的球心在线段OO'中点O1，
∵OA=
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
∴O1A=
| OO12+OA2 |
|
| ||
| 3 |
因此，正三棱柱的外接球半径R=
| ||
| 3 |
| 28 |
| 3 |
故选：C
点评：本题给出所有棱长均为2的正三棱柱，求它的外接球的表面积，着重考查了正三棱柱的性质、球的内切外接性质和球的表面积公式等知识，属于基础题．
练习册系列答案
相关题目
若一个正三棱柱的三视图如图所示，则这个正三棱柱的高和底面边长分别为（ ）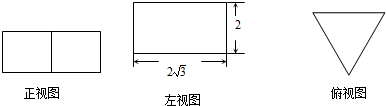
A、2，2
| ||
B、2
| ||
| C、4，2 | ||
| D、2，4 |
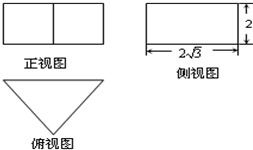若一个正三棱柱的三视图如图所示，则这个正三棱柱的高和底面边长分别为
