题目内容
已知双曲线![]() 的两个焦点为F:(-2,0),F:(2,0),点P(3,
的两个焦点为F:(-2,0),F:(2,0),点P(3,![]() )的曲线C上.
)的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
答案:
解析:
解析:
|
(Ⅰ)解:依题意,由a2+b2=4,得双曲线方程为 将点(3, 故所求双曲线方程为 (Ⅱ)解:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理, 得(1-k2)x2-4kx-6=0. ∵直线I与双曲线C相交于不同的两点E、F, ∴ ∴k∈(- 设E(x1,y1),F(x2,y2),则由①式得x1+x2= |EF|= = 而原点O到直线l的距离d= ∴SΔOEF= 若SΔOEF= 满足②,故满足条件的直线l有两条,其方程分别为y= |

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知双曲线的两个焦点为F1(-
,0)、F2(
,0),P是此双曲线上的一点,且PF1⊥PF2,|PF1|•|PF2|=2,则该双曲线的方程是( )
| 5 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
已知双曲线的两个焦点是椭圆
+
=1的两个顶点,双曲线的两条准线经过椭圆的两个焦点,则此双曲线的方程是( )
| x2 |
| 100 |
| y2 |
| 64 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
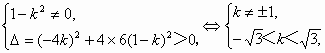
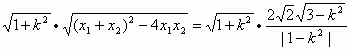
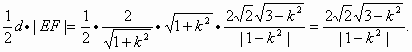
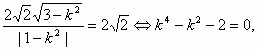 解得k=±
解得k=±