题目内容
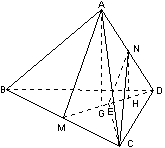
已知空间四边形ABCD中,AB=BC=CD=DA=DB=AC,M、N分别为BC、AD的中点。
求:AM与CN所成的角的余弦值;
![]()
解析:
(1)连接DM,过N作NE∥AM交DM于E,则∠CNE
为AM与CN所成的角。
∵N为AD的中点, NE∥AM省 ∴NE=![]() AM且E为MD的中点。
AM且E为MD的中点。
 设正四面体的棱长为1, 则NC=
设正四面体的棱长为1, 则NC=![]() ·
·![]() =
= ![]() 且ME=
且ME=![]() MD=
MD=![]()
在Rt△MEC中,CE2=ME2+CM2=![]() +
+![]() =
=![]()
∴cos∠CNE=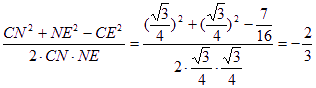 ,
,
又∵∠CNE ∈(0, ![]() )
)
∴异面直线AM与CN所成角的余弦值为![]() .
.
注:1、本题的平移点是N,按定义作出了异面直线中一条的平行线,然后先在△CEN外计算CE、CN、EN长,再回到△CEN中求角。
2、作出的角可能是异面直线所成的角,也可能是它的邻补角,在直观图中无法判定,只有通过解三角形后,根据这个角的余弦的正、负值来判定这个角是锐角(也就是异面直线所成的角)或钝角(异面直线所成的角的邻补角)。最后作答时,这个角的余弦值必须为正。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:
