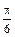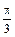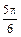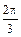题目内容
在极坐标系中,曲线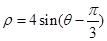 关于
关于
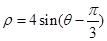 关于
关于A.点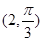 中心对称 中心对称 | B.直线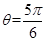 对称 对称 |
C.直线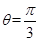 对称 对称 | D.极点中心对称 |
B
分析:先将原极坐标方程
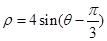 中的三角函数式利用差角公式展开后两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行求解即可.
中的三角函数式利用差角公式展开后两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行求解即可.解:将原极坐标方程
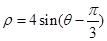 ,化为:
,化为:ρ2=2ρsinθ-2
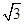 ρcosθ,
ρcosθ,化成直角坐标方程为:x2+y2+2
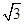 x-2y=0,
x-2y=0,是一个圆心在(-
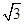 ,1),经过圆心的直线的极坐标方程是直线
,1),经过圆心的直线的极坐标方程是直线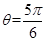 轴对称.
轴对称.故选B.

练习册系列答案
相关题目
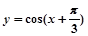 的图象,只需将函数
的图象,只需将函数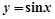 的图像 ( )
的图像 ( )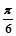 个长度单位
个长度单位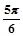 个长度单位。
个长度单位。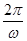
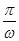
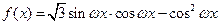
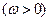 最小正周期为
最小正周期为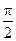 .
.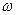 的值及函数
的值及函数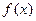 的解析式;
的解析式;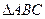 的三条边
的三条边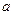 ,
,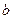 ,
,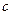 满足
满足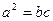 ,
,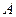 .求角
.求角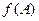 的值域.
的值域.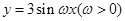 在区间
在区间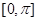 恰有
恰有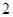 个零点,
个零点,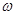 的取值范围为
的取值范围为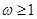
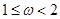
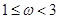
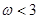

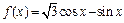 的图象向右平移
的图象向右平移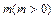 个单位长度后,所得图象对应的函
个单位长度后,所得图象对应的函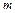 的最小值是
的最小值是