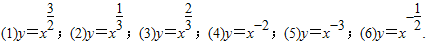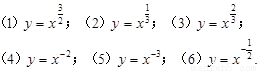题目内容
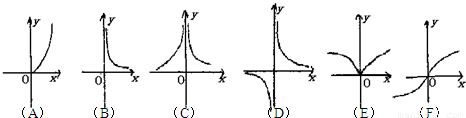
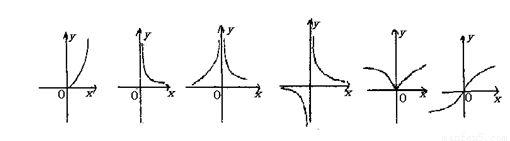
下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系

|

分析:根据函数的解析式确定函数的奇偶性和单调性,从而找到它对应的函数图象.
解答:解:六个幂函数的定义域,奇偶性,单调性如下:
(1)y=x
=
定义域[0,+∞),既不是奇函数也不是偶函数,在[0,+∞)是增函数;
通过上面分析,可以得出对应关系为:(1)?(A),(2)?(F),(3)?(E),(4)?(C),(5)?(D),(6)?(B).
(1)y=x
| 3 |
| 2 |
| x3 |
|
通过上面分析,可以得出对应关系为:(1)?(A),(2)?(F),(3)?(E),(4)?(C),(5)?(D),(6)?(B).
点评:本题主要考查幂函数的图象和性质,函数的单调性和奇偶性的应用,属于基础题.

练习册系列答案
相关题目
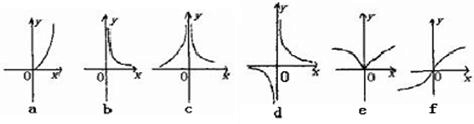
下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系,其中正确的对应选项是( )(1)y=x
;(2)y=x
;(3)y=
;(4)y=x-2;(5)y=x-3;(6)y=x-
.
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |

| A、(1)a,(2)f,(3)c,(4)e,(5)d,(6)b |
| B、(1)a,(2)f,(3)e,(4)c,(5)d,(6)b |
| C、(1)a,(2)b,(3)e,(4)c,(5)d,(6)f |
| D、(1)a,(2)f,(3)d,(4)c,(5)e,(6)b |
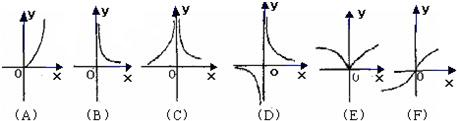
下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.( )
(1)y=x
;(2)y=x
;(3)y=x
;(4)y=x-2;(5)y=x-3;(6)y=x-
.
(1)y=x
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |

| A、(1)?(A),(2)?(F),(3)?(E),(4)?(C),(5)?(D),(6)?(B) |
| B、(1)?(B),(2)?(E),(3)?(C),(4)?(D),(5)?(A),(6)?(F) |
| C、(1)?(A),(2)?(E),(3)?(B),(4)?(D),(5)?(C),(6)?(F) |
| D、(1)?(B),(2)?(F),(3)?(A),(4)?(C),(5)?(D),(6)?(E) |