题目内容
己知函数f(x)=log2(-x2+2x+3)的定义域为A,函数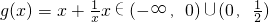 的值域为B,不等式2x2+mx-8<0的解集为C
的值域为B,不等式2x2+mx-8<0的解集为C
(1)求A∪(CRB)、A∩B;
(2)若A∩B⊆C,求m的取值范围.
解:(1)由-x2+2x+3>0 解得 A=(-1,3).由g(x)的解析式和定义域可得
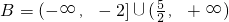 ,∴
,∴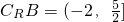 ,
,
 .
.
(2)因为A∩B⊆C,设h(x)=2x2+mx-8,由h(x)的图象可知;
方程的小根小于或等于 ,大根大于或等于3时,即可满足A∩B⊆C,∴
,大根大于或等于3时,即可满足A∩B⊆C,∴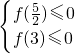 ,
,
即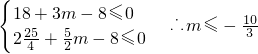 .
.
分析:(1)由-x2+2x+3>0 解得 A,由g(x)的解析式和定义域求得值域B,利用补集、两个集合的交集的定义
求出A∪(CRB)、A∩B.
(2)设h(x)=2x2+mx-8,由h(x)的图象可知,方程的小根小于或等于 ,大根大于或等于3,得到
,大根大于或等于3,得到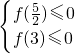 ,解不等式求得m的取值范围.
,解不等式求得m的取值范围.
点评:本题考查求函数的定义域,值域的方法,集合间的交,并,补混合运算,集合关系中参数的取值范围,求出A∩B
是解题的关键.
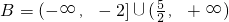 ,∴
,∴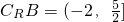 ,
, .
.(2)因为A∩B⊆C,设h(x)=2x2+mx-8,由h(x)的图象可知;
方程的小根小于或等于
 ,大根大于或等于3时,即可满足A∩B⊆C,∴
,大根大于或等于3时,即可满足A∩B⊆C,∴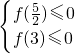 ,
,即
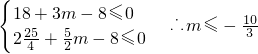 .
.分析:(1)由-x2+2x+3>0 解得 A,由g(x)的解析式和定义域求得值域B,利用补集、两个集合的交集的定义
求出A∪(CRB)、A∩B.
(2)设h(x)=2x2+mx-8,由h(x)的图象可知,方程的小根小于或等于
 ,大根大于或等于3,得到
,大根大于或等于3,得到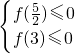 ,解不等式求得m的取值范围.
,解不等式求得m的取值范围.点评:本题考查求函数的定义域,值域的方法,集合间的交,并,补混合运算,集合关系中参数的取值范围,求出A∩B
是解题的关键.

练习册系列答案
相关题目